题目内容
12.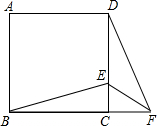 如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C按顺时针方向旋转90°得到△DCF,连接EF,则∠EFC的度数为( )
如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C按顺时针方向旋转90°得到△DCF,连接EF,则∠EFC的度数为( )| A. | 25° | B. | 30° | C. | 45° | D. | 60° |
分析 由旋转前后的对应角相等可知,CF=CE;一个特殊三角形△ECF为等腰直角三角形,可知∠EFC的度数.
解答 解:∵△DCF是△BCE旋转以后得到的图形,
∴CF=CE.
又∵∠ECF=90°,
∴∠EFC=∠FEC=$\frac{1}{2}$(180°-∠ECF)=$\frac{1}{2}$(180°-90°)=45°.
故选:C.
点评 本题考查了图形的旋转变化,由旋转的性质得出△ECF为等腰直角三角形是解题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
2.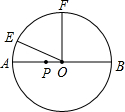 已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )
已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )
 已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )
已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )| A. | 5cm | B. | 5$\sqrt{2}$cm | C. | 5$\sqrt{3}$cm | D. | 10cm |
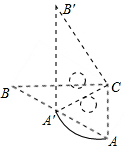 如图,△ABC和△A′B′C′是两个完全重合的直角三角板,∠B=30°,斜边长为10cm,三角板A′B′C′绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长是多少?
如图,△ABC和△A′B′C′是两个完全重合的直角三角板,∠B=30°,斜边长为10cm,三角板A′B′C′绕直角顶点C顺时针旋转,当点A′落在AB边上时,CA′旋转所构成的扇形的弧长是多少?