题目内容
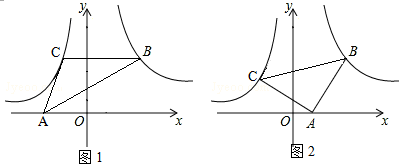
14.已知点A(-3,a),B(-1,b),C(3,c)都在反比例函数y=$\frac{m}{x}$(m为常数,m<0)上,则a,b,c的大小关系为c<a<b.分析 先根据反比例函数中m<0判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
解答 解:∵反比例函数y=$\frac{m}{x}$中m<0,
∴函数图象的两个分支分别位于二、四象限,且在每一象限内y随x的增大而增大.
∵-2<-1<0,
∴A(-3,a),B(-1,b)位于第二象限,且0<a<b.
∵3>0,
∴点C(3,c)位于第四象限,
∴c<0,
∴c<a<b.
故答案为:c<a<b.
点评 本题考查的是反比例函数图象上点的坐标特征,解题时,利用了反比例函数图象的增减性,减少了繁琐的计算过程.

练习册系列答案
相关题目
2.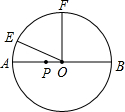 已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )
已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )
 已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )
已知:如图,点E、F是半径为5cm的⊙O上两定点,点P是直径AB上的一动点,AB⊥OF,∠AOE=30°,则点P在AB上移动的过程中,PE+PF的最小值是( )| A. | 5cm | B. | 5$\sqrt{2}$cm | C. | 5$\sqrt{3}$cm | D. | 10cm |
9.若y=(m-1)x|m|-2是反比例函数,则m的值为( )
| A. | m=2 | B. | m=-1 | C. | m=1 | D. | m=0 |
7.下列各式计算正确的是( )
| A. | (xy2)3=xy6 | B. | (3ab)2=6a2b2 | C. | (-2x2)2=-4x4 | D. | (a2b3)m=a2mb3m |
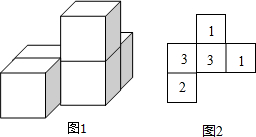 (1)如图1所示,是用五个小正方体搭成的几何体,请画出它的三视图.
(1)如图1所示,是用五个小正方体搭成的几何体,请画出它的三视图.