题目内容
19.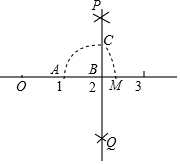 如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
分析 直接利用勾股定理得出OC的长,进而得出答案.
解答 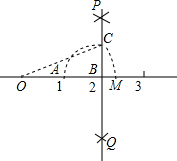 解:如图所示:连接OC,
解:如图所示:连接OC,
由题意可得:OB=2,BC=1,
则OC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
故点M对应的数是:$\sqrt{5}$.
故选:B.
点评 此题主要考查了勾股定理,根据题意得出CO的长是解题关键.

练习册系列答案
相关题目
14.已知等边三角形的边长为3,点P为等边三角形内任意一点,则点P到三边的距离之和为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | 不能确定 |
4.下列计算正确的是( )
| A. | (a2)3=a5 | B. | (-2a)2=-4a2 | C. | m3•m2=m6 | D. | a6÷a2=a4 |
11.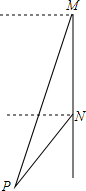 如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
 如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )
如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)( )| A. | 22.48 | B. | 41.68 | C. | 43.16 | D. | 55.63 |
8.二次函数y=2x2-3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
| A. | 抛物线开口向下 | B. | 抛物线经过点(2,3) | ||
| C. | 抛物线的对称轴是直线x=1 | D. | 抛物线与x轴有两个交点 |
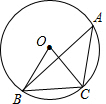 如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=35°.
如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=35°.