题目内容
6.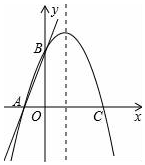 如图,已知直线y=3x+3与x轴交于点A,与y轴交于点B,过A,B两点的抛物线交x轴于另一点C(3,0).
如图,已知直线y=3x+3与x轴交于点A,与y轴交于点B,过A,B两点的抛物线交x轴于另一点C(3,0).(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△ABP是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,说明理由.
(3)在抛物线上求一点Q,使得△ACQ为等腰三角形,并写出Q点的坐标;
(4)除(3)中所求的Q点外,在抛物线上是否还存在其它的点Q使得△ACQ为等腰三角形?若存在,请求出一共有几个满足条件的点Q(要求简要说明理由,但不证明);若不存在这样的点Q,请说明理由.
分析 (1)先求得点A和点B的坐标,然后设抛物线的解析式为y=a(x+1)(x-3),将点B的坐标代入求解即可;
(2)抛物线的对称轴为x=1.设点P的坐标为(1,a),分为AB=AP、BA=BP、AP=BP三种情况,然后结合两点间的距离公式列方程求解即可;
(3)当点Q在AC的垂直平分线上时,QA=QC,即点Q为抛物线的顶点;
(4)由(3)可知当Q为抛物线的顶点时,△AQC为等腰三角形;以A为圆心,以AC长为半径作⊙A,⊙A交抛物线与Q1、Q2、Q3,以C为圆心,AC长为半径作⊙C,交抛物线与点Q4、Q5、Q6,依据图形可得到问题的答案.
解答 解:(1)令x=0得:y=3,
∴B(0,3).
令y=0得:3x+3=0,解得x=-1,
∴A(-1,0).
设抛物线的解析式为y=a(x+1)(x-3),将点B的坐标代入得:-3a=3,解得a=-1,
∴抛物线的解析式为y=-x2+2x+3.
(2)抛物线的对称轴方程为x=-$\frac{2}{-1×2}$=1.
设点P的坐标为(1,a).
当AB=AP时,$\sqrt{(-1-0)^{2}+(3-0)^{2}}$=$\sqrt{(-1-1)^{2}+(a-0)^{2}}$,整理得:10=4+a2,解得a=±$\sqrt{6}$
∴P(1,$\sqrt{6}$)或(1,-$\sqrt{6}$).
当BA=BP时,$\sqrt{(-1-0)^{2}+(3-0)^{2}}$=$\sqrt{{1}^{2}+(3-a)^{2}}$,整理得:10=1+(3-a)2,解得:a=0或a=6,
∴P(1,0)或(1,6).
当AP=BP时,$\sqrt{(-1-1)^{2}+(a-0)^{2}}$=$\sqrt{{1}^{2}+(3-a)^{2}}$,整理得:6a=6,解得a=1,
∴P(1,1).
综上所述:点P的坐标为P(1,$\sqrt{6}$)或(1,-$\sqrt{6}$)或P(1,0)或(1,6)或P(1,1).
(3)当点Q在AC的垂直平分线上时,则QA=QC.
由抛物线的对称性可知:此时点Q为抛物线的顶点.
∵y=-x2+2x+3=-(x-1)2+4,
∴Q(1,4).
(4)当QA=QC,时,抛物线的顶点即为所求的点Q.
如图所示:以A为圆心,以AC长为半径作⊙A,⊙A交抛物线与Q1、Q2、Q3,以C为圆心,AC长为半径作⊙C,交抛物线与点Q4、Q5、Q6.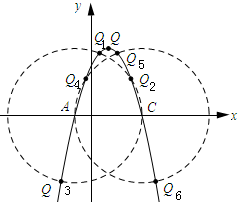
由圆的性质可知:△ACQ1、△ACQ2、△ACQ3、△ACQ4、△ACQ5、△ACQ6均为等腰三角形.
∴符合题意的点Q共有7个.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数解析式,点的坐标与函数解析式之间的关系,二次函数的图象和性质,分为讨论是解答问题(2)的关键;作出⊙A和⊙C依据圆的性质和二次函数的性质判定出点Q的个数是解答问题(3)的关键.

| A. | 斜边及一锐角分别相等的两个直角三角形全等 | |
| B. | 两条直角边分别相等的两个直角三角形全等 | |
| C. | 两个锐角分别相等的两个直角三角形全等 | |
| D. | 一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等 |
 把如图所示的纸片折成一个如图2所示的正方体,则从该正方体左侧看到的面上的字是( )
把如图所示的纸片折成一个如图2所示的正方体,则从该正方体左侧看到的面上的字是( )| A. | 祝 | B. | 试 | C. | 顺 | D. | 利 |
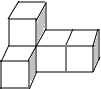 如图是由5个大小相同的小正方体拼成的几何体,下列说法中,正确的是( )
如图是由5个大小相同的小正方体拼成的几何体,下列说法中,正确的是( )| A. | 主视图是轴对称图形 | B. | 左视图是轴对称图形 | ||
| C. | 俯视图是轴对称图形 | D. | 三个视图都不是轴对称图形 |
| A. | 不断变大 | B. | 不断减小 | C. | 不变 | D. | 不能确定 |
 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度匀速,过点P作PD∥BC,交AB于点D,连结PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0)
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度匀速,过点P作PD∥BC,交AB于点D,连结PQ,点P、Q分别从点A、C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0)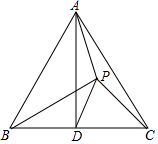 如图,△ABC是等边三角形,点D为BC的中点,点P在△ABC的内部,连接PA、PB、PC、PD,∠BPC=105°,PC=2,PB=2$\sqrt{2}$,则△APD的面积为$\frac{1}{2}\sqrt{3}$.
如图,△ABC是等边三角形,点D为BC的中点,点P在△ABC的内部,连接PA、PB、PC、PD,∠BPC=105°,PC=2,PB=2$\sqrt{2}$,则△APD的面积为$\frac{1}{2}\sqrt{3}$. 解决问题:如图,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是10$\sqrt{2}$+8.
解决问题:如图,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是10$\sqrt{2}$+8.