题目内容
5.某户外用品店准备购进甲、乙两种登山包,.其中甲种比乙种登山包每个进价高20元,甲、乙两种登山包的售价分别为240元/个、160元/个.用1000元购进甲种个数与用800元购进乙种的个数相同(1)求甲、乙两种登山包的进价分别为多少?
(2)如果购进的甲、乙两种登山包共200个,其中甲种登山包的个数不多于105个,总利润(不计其他成本)不少于21700元,那么该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种登山包进行优惠促销活动,决定对甲种登山包每个优惠安原售价七折出售,乙种登山包价格不变.那么该专卖店要获得最大利润应如何进货?
分析 (1)设乙种登山包每个进价x元,则甲种登山包每个进价为(x+20)元.根据1000元购进甲种个数与用800元购进乙种的个数相同,列出方程即可解决问题;
(2)设购进的甲种登山包a个,则购进乙种登山包(200-a)个.列出不等式组即可解决问题;
(3)构建一次函数,利用一次函数的增减性即可解决问题;
解答 解:(1)设乙种登山包每个进价x元,则甲种登山包每个进价为(x+20)元.
由题意$\frac{1000}{x+20}$=$\frac{800}{x}$,
解得x=80,
经检验,x=80是分式方程的解.
答:甲、乙两种登山包的进价分别为100元和80元.
(2)设购进的甲种登山包a个,则购进乙种登山包(200-a)个.
由题意$\left\{\begin{array}{l}{a≤105}\\{140a+80(200-a)≥21700}\end{array}\right.$,
解得95≤a≤105,
∵a是整数,
∴a=95,96,97,98,99,100,101,102,103,104,105.
∴一共有11种方案.
(3)设总利润为w,则w=68a+80(200-a)=-12a+16000(95≤a≤105),
∵-12<0,
∴w随a的增大而减小,
∴x=95时,w最大,
∴该专卖店要获得最大利润应购进的甲种登山包95个,购进乙种登山包105个.
点评 本题考查一次函数的应用、分式方程的应用、一元一次不等式组的应用等整数,解题的关键是学会设未知数,构建方程或不等式解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 已知二次函数y=ax2+bx+c的图象如图所示,则( )
已知二次函数y=ax2+bx+c的图象如图所示,则( )
 已知二次函数y=ax2+bx+c的图象如图所示,则( )
已知二次函数y=ax2+bx+c的图象如图所示,则( )| A. | b>0,c>0 | B. | b>0,c<0 | C. | b<0,c<0 | D. | b<0,c>0 |
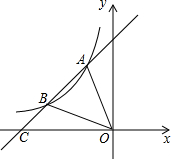 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{m}{x}$图象相交于点A(-1,2)
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{m}{x}$图象相交于点A(-1,2)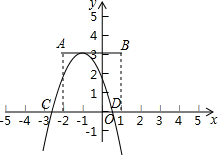 如图,点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动,形状保持不变,且与x轴交于C、D两点,(C在D左侧).若点D的横坐标最大值为5,则点C的横坐标最小值为-6.
如图,点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动,形状保持不变,且与x轴交于C、D两点,(C在D左侧).若点D的横坐标最大值为5,则点C的横坐标最小值为-6.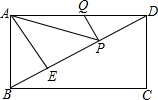 如图,在矩形ABCD中,AB=3,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD、AD上,则AP+PQ最小值为$\frac{9}{2}$.
如图,在矩形ABCD中,AB=3,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD、AD上,则AP+PQ最小值为$\frac{9}{2}$.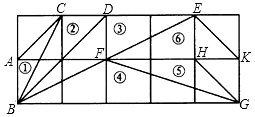 如图,在正方形网格上有6个三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.
如图,在正方形网格上有6个三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.