题目内容
13.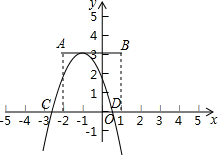 如图,点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动,形状保持不变,且与x轴交于C、D两点,(C在D左侧).若点D的横坐标最大值为5,则点C的横坐标最小值为-6.
如图,点A,B的坐标分别为(-2,3)和(1,3),抛物线y=ax2+bx+c(a<0)的顶点在线段AB上运动,形状保持不变,且与x轴交于C、D两点,(C在D左侧).若点D的横坐标最大值为5,则点C的横坐标最小值为-6.
分析 根据题意得出点C的横坐标最小抛物线解析式,进而得出点C的横坐标最小值.
解答 解:∵点D的横坐标最大值为5,此时抛物线顶点为:(1,3),
∴y=a(x-1)2+3,
将(5,0)代入得:0=a(5-1)2+3,
解得:a=-$\frac{3}{16}$,
故抛物线解析式为:y=-$\frac{3}{16}$(x-1)2+3,
当点C的横坐标最小,则抛物线解析式为:y=-$\frac{3}{16}$(x+2)2+3,
当y=0时,x1=-6,x2=-2,
故点C的横坐标最小值为:-6.
故答案为:-6.
点评 此题主要考查了抛物线与x轴的交点以及二次函数的最值,正确得出抛物线解析式是解题关键.

练习册系列答案
相关题目
 如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为π-2.
如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分的面积为π-2.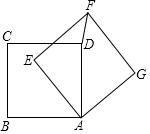 如图,正方形AEFG与正方形ABCD的边长都为2,正方形AEFG绕正方形ABCD的顶点A旋转一周,在此旋转过程中,线段DF的长可取的整数值可以为1或2或3或4.
如图,正方形AEFG与正方形ABCD的边长都为2,正方形AEFG绕正方形ABCD的顶点A旋转一周,在此旋转过程中,线段DF的长可取的整数值可以为1或2或3或4.