题目内容
17.解不等式组:$\left\{\begin{array}{l}{1-2x≤3}\\{x+1<3(3-x)}\end{array}\right.$,并写出它的整数解.分析 首先解出不等式组的各个不等式x的取值范围,然后求出x的公共部分,即可求得整数解.
解答 解:$\left\{\begin{array}{l}{1-2x≤3①}\\{x+1<3(3-x)②}\end{array}\right.$
由①得:x≥-1;
由②得:x<2;
∴不等式组的解集是-1≤x<2,
∴符号条件的整数解为-1,0,1.
点评 本题主要考查解一元一次不等式组,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
18.若正多边形的一个内角是150°,则该正多边形的边数是( )
| A. | 6 | B. | 12 | C. | 16 | D. | 18 |
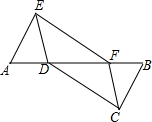 如图,四边形CDEF是平行四边形,点A、B在直线DF上,已知FB=AD,连接AE、BC.
如图,四边形CDEF是平行四边形,点A、B在直线DF上,已知FB=AD,连接AE、BC.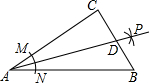 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交变BC于点D,若CD=4,AB=15,求△ABD的面积.
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交变BC于点D,若CD=4,AB=15,求△ABD的面积.