题目内容
如图，在△ABC中，∠BAC的平分线交BC于点D，AB：AC=m：n（m＜n），CD-BD=a，求BC的长．考点：平行线分线段成比例
专题：
分析：过C作CE∥AB，交AD的延长线于点E，则可得△ABD∽△ECD，可知
=
，再结合角平分线可得∠CAD=∠CED，所以AC=EC，可求得
=
，且CD-BD=a，可求得CD和BD，进一步可求得BC的长．
| AB |
| CE |
| BD |
| CD |
| BD |
| CD |
| m |
| n |
解答：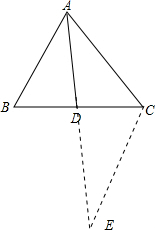
解：
过C作CE∥AB，交AD的延长线于点E，
则△ABD∽△ECD，
∴
=
，
∵CE∥AB，
∴∠BAD=∠E，
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠CAD=∠E，
∴CE=AC，
∴
=
=
，
且CD-BD=a，
可解得CD=
，BD=
，
∴BC=BD+CD=
．
解：过C作CE∥AB，交AD的延长线于点E，
则△ABD∽△ECD，
∴
| AB |
| CE |
| BD |
| CD |
∵CE∥AB，
∴∠BAD=∠E，
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠CAD=∠E，
∴CE=AC，
∴
| BD |
| CD |
| AB |
| AC |
| m |
| n |
且CD-BD=a，
可解得CD=
| an |
| n-m |
| am |
| n-m |
∴BC=BD+CD=
| a(m+n) |
| n-m |
点评：本题主要考查相似三角形的判定和性质及等腰三角形的判定和性质，利用条件把BD：CD转化为AB：AC是解题的关键．
练习册系列答案
相关题目
有理数a、b、c在数轴上的位置如图所示，化简：-|c-a|+|b|+|a|-|c|=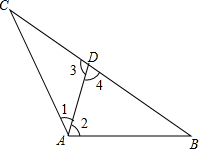
写出如图的符合下列条件的角．（图中所有的角均指小于平角的角）．