题目内容
14.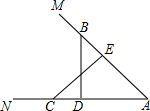 已知,如图,点B、C分别在∠MAN的两边上,BD⊥AN,CE⊥AM,垂足分别为D、E,BD、CE相交于点F,且BE=CD,求证:点F在∠MAN的平分线上.
已知,如图,点B、C分别在∠MAN的两边上,BD⊥AN,CE⊥AM,垂足分别为D、E,BD、CE相交于点F,且BE=CD,求证:点F在∠MAN的平分线上.
分析 证明△BFE≌△CFD,则EF=DF,又BD⊥AN,CE⊥AM,则点F在∠MAN的平分线上.
解答 证明:∵BD⊥AN,CE⊥AM,
∴∠BEF=∠CDF=90°,
在△BFE和△CFD中,
$\left\{\begin{array}{l}{∠BEF=∠CDF}\\{∠BFE=∠CFD}\\{BE=CD}\end{array}\right.$,
∴△BFE≌△CFD,
∴EF=DF,
又∵BD⊥AN,CE⊥AM,
∴点F在∠MAN的平分线上.
点评 本题主要考查了全等三角形的判定与性质以及角平分线的判定,熟练掌握全等三角形的判定与性质以及角平分线的性质与判定是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在同一直角坐标系中,P、Q分别是y=-x+3与y=3x-5的图象上的点,且P、Q关于x轴对称,则点P的坐标是( )
| A. | (-$\frac{1}{2}$,$\frac{7}{2}$) | B. | (-2,5) | C. | (1,2) | D. | (-4,7) |
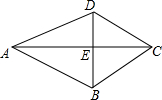 如图,△ADE≌△ABE,△DCE≌△BCE,求证:△ADC≌△ABC.
如图,△ADE≌△ABE,△DCE≌△BCE,求证:△ADC≌△ABC.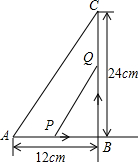 如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以2cm/s的速度移动,Q从点B开始沿BC向C点以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于16cm2?
如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以2cm/s的速度移动,Q从点B开始沿BC向C点以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,几秒钟后,△PBQ的面积等于16cm2? 如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图: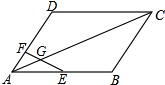 如图,在?ABCD中,E为AB的中点,点F在AD上,EF交AC于点G,AF=2,DF=4,AG=3,求AC的长.
如图,在?ABCD中,E为AB的中点,点F在AD上,EF交AC于点G,AF=2,DF=4,AG=3,求AC的长.