题目内容
4.已知反比例函数y=$\frac{2k}{x}$,当x<0时,y随x增大而减小,与直线y=-x+$\sqrt{3}k$都过点P,且OP=$\sqrt{7}$,则k的值为$\frac{7}{3}$.分析 设出P的坐标为(a,b),由P为两函数的交点,将P坐标代入反比例与直线解析式中,得到ab与a+b,再利用勾股定理表示出|OP|,代入OP=$\sqrt{7}$中,利用完全平方公式变形,把表示出的ab与a+b代入,得到关于k的方程,求出方程的解即可得到k的值.
解答 解:设P坐标为(a,b),代入反比例解析式得:ab=2k;代入直线解析式得:a+b=$\sqrt{3}$k,
∵OP=$\sqrt{7}$,
∴a2+b2=(a+b)2-2ab=($\sqrt{3}$k)2-2×2k=($\sqrt{7}$)2,
整理得:3k2-4k-7=0
解得:k1=-1,k2=$\frac{7}{3}$,
∵反比例函数y=$\frac{2k}{x}$,当x<0时,y随x增大而减小,
∴k>0,
∴k=-1(不合题意,舍去),
∴k=$\frac{7}{3}$.
故答案为:$\frac{7}{3}$.
点评 此题考查了反比例函数与一次函数的交点问题,涉及的知识有:勾股定理,完全平方公式的运用,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
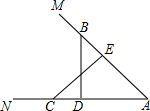 已知,如图,点B、C分别在∠MAN的两边上,BD⊥AN,CE⊥AM,垂足分别为D、E,BD、CE相交于点F,且BE=CD,求证:点F在∠MAN的平分线上.
已知,如图,点B、C分别在∠MAN的两边上,BD⊥AN,CE⊥AM,垂足分别为D、E,BD、CE相交于点F,且BE=CD,求证:点F在∠MAN的平分线上.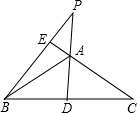 如图,在等腰三角形ABC中,AD、BE分别是底边BC和腰AC上的高线,DA、BE的延长线交于点P.若∠BAC=110°,求∠P的度数.
如图,在等腰三角形ABC中,AD、BE分别是底边BC和腰AC上的高线,DA、BE的延长线交于点P.若∠BAC=110°,求∠P的度数.
 等腰△ABC的顶角为36°,BC沿CD对折,点B交AC于E,求DE与AD的比值.
等腰△ABC的顶角为36°,BC沿CD对折,点B交AC于E,求DE与AD的比值.