题目内容
5.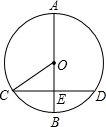 如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )
如图,已知AB是⊙O的直径,弦CD⊥AB于点E,若AB=6cm,CD=4cm,则sin∠OCE等于( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{3}$ |
分析 先根据垂径定理求出CE的长,再根据勾股定理得出OE的长,根据锐角三角函数的定义即可得出结论.
解答 解:∵直径AB⊥CD于E,CD=4,
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}×4$=2,
∵AB=6,
∴OC=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3,
∴OE=$\sqrt{{OC}^{2}{-CE}^{2}}$=$\sqrt{{3}^{2}{-2}^{2}}$=$\sqrt{5}$,
∴sin∠OCE=$\frac{OE}{OC}$=$\frac{\sqrt{5}}{3}$,
故选D.
点评 本题主要考查了垂径定理,勾股定理及锐角三角函数的定义,熟知垂直于弦的直径平分弦是解答此题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
15.已知,△ABC∽△DEF,△ABC与△DEF的面积之比为1:2,当BC=1,对应边EF的长是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
20.以下叙述中错误的是( )
| A. | $±\sqrt{0.25}$=±0.5 | B. | $±\sqrt{0.25}$=0.5 | C. | 0的平方根是0 | D. | 1是1的平方根 |
10.学校组织了一次游戏,每位选手朝特制的靶子上各投三以飞镖,现规定,当飞镖落在同一圆环内时得分相同.如图所示,小明、小君、小红的成绩分别是29分、43分和33分,则小华的成绩是( )


| A. | 31分 | B. | 33分 | C. | 36分 | D. | 38分 |
14.下列计算正确的是( )
| A. | x2•x3=x3 | B. | (mn)2=mn2 | C. | (-x5)4=x20 | D. | (a2)3=a5 |
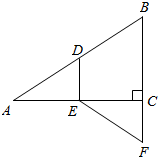 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=$\frac{1}{2}$BC.若AB=12,求EF的长.
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=$\frac{1}{2}$BC.若AB=12,求EF的长.