题目内容
6.下列各数中:0,$\sqrt{8}$,1.3030030003…(每两个3之间多一个0),-1+$\sqrt{4}$,1.$\stackrel{•}{5}$4$\stackrel{•}{2}$,$\root{3}{-27}$,$\frac{22}{7}$,π2-3,无理数的个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 无理数就是无限不循环小数,依据定义即可判断.
解答 解:无理数有:$\sqrt{8}$,1.3030030003…(每两个3之间多一个0),π2-3共4个.
故选C.
点评 此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,$\sqrt{6}$,0.8080080008…(每两个8之间依次多1个0)等形式.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
17.下列说法中,正确的是( )
| A. | $\sqrt{16}$=±4 | B. | -22的平方根是±2 | ||
| C. | 64的立方根是±4 | D. | -$\sqrt{5}$是5的一个平方根 |
18.若(a2+1)2-2(a2+1)-3=0,则a2等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 以上都不对 |




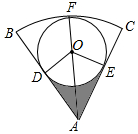 如图,AB,AC是扇形的两条半径,⊙O分别与AB,AC相切于点D,E,与$\widehat{BC}$相切于点F,若⊙O的面积是4π,∠A=60°,求图形阴影部分的面积.
如图,AB,AC是扇形的两条半径,⊙O分别与AB,AC相切于点D,E,与$\widehat{BC}$相切于点F,若⊙O的面积是4π,∠A=60°,求图形阴影部分的面积.