题目内容
11.数学老师在课堂上提出一个问题:“通过探究知道:$\sqrt{2}$≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用$\sqrt{2}$-1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答:(1)$\sqrt{5}$的小数部分是a,$\sqrt{37}$的整数部分是b,求a+b-$\sqrt{5}$的值.
(2)已知8+$\sqrt{3}$=x+y,其中x是一个整数,0<y<1,求3x+(y-$\sqrt{3}$)2015的值.
分析 (1)估算出$\sqrt{5}$和$\sqrt{37}$的大致范围,然后可求得a、b的值,然后再求代数式的值即可.
(2)先求得x的值,然后再表示出y-$\sqrt{3}$的值,最后进行计算即可.
解答 解:(1)∵4<5<9,36<37<49,
∴2<$\sqrt{5}$<3,6<$\sqrt{37}$<7.
∴a=$\sqrt{5}$-2,b=6.
∴a+b-$\sqrt{5}$=$\sqrt{5}$-2+6-$\sqrt{5}$=4.
(2)∵1<$\sqrt{3}$<2,
∴9<8+$\sqrt{3}$<10,
∴x=9.
∵y=8+$\sqrt{3}$-x.
∴y-$\sqrt{3}$=8-x=-1.
∴原式=3×9-1=26.
点评 本题主要考查的是估算无理数的大小,求得y-$\sqrt{3}$的值的大小是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
1.如果3xn-1y3与-5x3ym是同类项,则m和n的取值是( )
| A. | 3和-4 | B. | -3和4 | C. | 3和4 | D. | -3和-4 |
16.已知一个等腰三角形的腰长,底边长满足x2+y2-6x-12y+45=0,则这个等腰三角形的周长是( )
| A. | 12 | B. | 15 | C. | 12或15 | D. | 45 |
3.若a3(3an-2am+4ak)=3a9-2a6+4a4,则m,n,k的值分别为( )
| A. | 6,3,1 | B. | 3,6,1 | C. | 2,1,3 | D. | 2,3,1 |
 我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律.
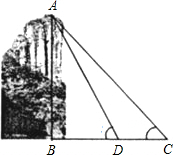 如图,为测得峰顶A到河面B的高度,当游船行至C处时测得峰顶A的仰角为45°,前进20米至D处时测得峰顶A的仰角为60°(此时C、D、B三点在同一直线上),求峰顶A到河面B的高度.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$=1.73)
如图,为测得峰顶A到河面B的高度,当游船行至C处时测得峰顶A的仰角为45°,前进20米至D处时测得峰顶A的仰角为60°(此时C、D、B三点在同一直线上),求峰顶A到河面B的高度.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$=1.73)