题目内容
4.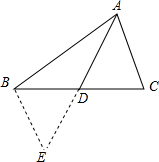 如图,AD为△ABC的中线,已知AD=4cm,试确定AB+AC的取值范围.
如图,AD为△ABC的中线,已知AD=4cm,试确定AB+AC的取值范围.解:延长AD到E,使DE=AD,连接BE.
因为AD为△ABC的中线,
所以BD=CD.
在△ACD和△EBD中,因为AD=DE,∠ADC=∠EDB,CD=BD,所以△ACD≌△EBD(SAS)
所以BE=CA(两三角形全等,对应边相等,)
因为AB+BE>AE(两边之和大于第三边,)
所以AB+AC>AE.
因为AE=2AD=8cm,
所以AB+AC>8cm.
分析 延长AD到E,使DE=AD,连接BE.因为AD为△ABC的中线,所以BD=CD,证明△ACD≌△EBD,由三角形的三边关系定理得出答案.
解答 解: 如图,延长AD到E,使DE=AD,连接BE.
如图,延长AD到E,使DE=AD,连接BE.
因为AD为△ABC的中线,
所以BD=CD.
在△ACD和△EBD中,因为AD=DE,∠ADC=∠EDB,CD=BD,所以△ACD≌△EBD(SAS)
所以BE=CA(两三角形全等,对应边相等,)
因为AB+BE>AE(两边之和大于第三边,)
所以AB+AC>AE.
因为AE=2AD=8cm,
所以AB+AC>8cm,
故答案为:SAS,两三角形全等,对应边相等,两边之和大于第三边,8.
点评 此题主要考查了全等三角形的判定与性质以及学生对三角形三边关系及中线的性质等的理解及运用能力,得出△ACD≌△EBD是解题关键.

练习册系列答案
相关题目
19.方程$2{x^2}-3x=\frac{1}{2}({{x^2}-6x})$的解是( )
| A. | 0,0 | B. | 0,3 | C. | 0,2 | D. | 0,$\frac{1}{3}$ |
16.下列各点中在抛物线y=x2-4x-4上的点是( )
| A. | (4,4) | B. | (3,-1) | C. | (-2,-8) | D. | (-$\frac{1}{2}$,-$\frac{7}{4}$) |
13.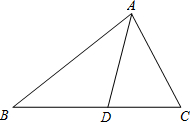 在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )
在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )
 在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )
在△ABC中,AD是∠BAC的平分线,且AB=AC+CD,若∠BAC=75°,则∠ABC的大小为( )| A. | 25° | B. | 35° | C. | 37.5° | D. | 45° |

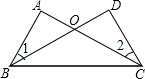 如图,AB=CD,AC=BD,求证:∠A=∠D,∠1=∠2.
如图,AB=CD,AC=BD,求证:∠A=∠D,∠1=∠2.