Question

14．小明做数学作业时遇到一道证明题：求证三角形的三条角平分线交于一点．
小明首先根据题意画出图形如图1．

然后他将原命题转化为：
已知：在△ABC中，∠ABC和∠ACB的平分线交于点I，求证：AI是∠BAC的角平分线．
（1）请帮小明补全命题的结论：AI是∠BAC的角平分线；
（2）结合图2，补全下面证明过程（括号中填写定理内容）
作IP⊥BC于点P，IQ⊥AC于点Q，IR⊥AB于点R．
∵BI平分∠ABC，IP⊥BC，IR⊥AB
∴IP=IR（角的平分线上的点，到角两边的距离相等）
同理：IP=IQ
∴IQ=IR
又∵IQ⊥AC，IR⊥AB
∴AI平分∠BAC（到角两边的距离相等的点在这个角的平分线上）
（3）根据上述结论，完成下述作图任务：
如图3，有一张矩形纸片，上面画有一个角的两边m，n，但是这个角的顶点P在纸片的外部，试在纸片上作出∠P的平分线．（要求：尺规作图，不得折纸，不得超出矩形纸片，保留作图痕迹，不必写作法）

Answer 1

分析 （1）把文字命题写成已知，求证即可解决问题．
（2）作IP⊥BC于点P，IQ⊥AC于点Q，IR⊥AB于点R．根据角平分线的性质定理以及判定定理即可证明．
（3）如图3中，设直线m与n交于点F，在直线m上取两点A、D，在直线n上取两点B、C，连接AB、CD．作∠FAB、∠FBA的角平分线交于点E，作∠FDC、∠FCD的角平分线交于点G，直线GE就是∠AFB的平分线．

解答 解：已知：在△ABC中，∠ABC和∠ACB的平分线交于点I，求证∠BAC的平分线．
故答案为∠BAC的平分线．
（1）题的结论：AI是∠BAC的平分线，
故答案为∠BAC的平分线．
（2）作IP⊥BC于点P，IQ⊥AC于点Q，IR⊥AB于点R．
∵BI平分∠ABC，IP⊥BC，IR⊥AB
∴IP=IR（角的平分线上的点，到角两边的距离相等）
同理：IP=IQ，
∴IQ=IR
又∵IQ⊥AC，IR⊥AB
∴AI平分∠BAC，（到角两边的距离相等的点在这个角的平分线上）
故答案分别为角的平分线上的点，到角两边的距离相等；  IP=IQ；IA是∠BAC的平分线；在角的内部到角两边的距离相等的点在角的平分线上．
（3）如图3中，设直线m与n交于点F，在直线m上取两点A、D，在直线n上取两点B、C，连接AB、CD．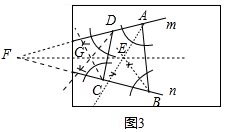

作∠FAB、∠FBA的角平分线交于点E，作∠FDC、∠FCD的角平分线交于点G，直线GE就是∠AFB的平分线．
所以图中直线EG即为所求．

点评 本题考查三角形综合题、角平分线的性质定理以及判定定理等知识，解题的关键是学会添加常用辅助线，熟练应用所学知识解决问题，第三个问题的突破点是找到角平分线上的两个点，即可解决问题．