题目内容
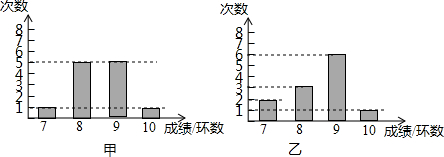
4.甲乙两人进行射击训练,两人分别射击12次,如图分别统计了两人的射击成绩,已知甲射击成绩的方差S甲2=$\frac{7}{12}$,平均成绩$\overline{{x}_{甲}}$=8.5.(1)根据图上信息,估计乙射击成绩不少于9环的概率是多少?
(2)求乙射击的平均成绩的方差,并据此比较甲乙的射击“水平”.
S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2…(xn-$\overline{x}$)2].
分析 (1)根据条形统计图求出乙的射击总数与不少于9环的次数,根据概率公式即可得出结论;
(2)求出乙的平均成绩及方差,再与甲的平均成绩及方差进行比较即可.
解答 解:(1)∵由图可知,乙射击的总次数是12次,不少于9环的有7次,
∴乙射击成绩不少于9环的概率=$\frac{7}{12}$;
(2)$\overline{{x}_{乙}}$=$\frac{2×7+3×8+6×9+1×10}{12}$=8.5(环),
${S}_{乙}^{2}$=$\frac{1}{12}$[(7-8.5)2×2+(8-8.5)2×3+(9-8.5)2×6+(10-8.5)2]
=$\frac{9}{12}$
=$\frac{3}{4}$.
∵$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${S}_{甲}^{2}$<${S}_{乙}^{2}$,
∴甲的射击成绩更稳定.
点评 本题考查的是概率公式,熟记随机事件的概率公式及方差的定义是解答此题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
19.下列运算正确的是( )
| A. | (-$\frac{3}{2}$)2=-$\frac{9}{4}$ | B. | (3a2)3=9a6 | C. | 5-3÷5-5=$\frac{1}{25}$ | D. | $\sqrt{8}-\sqrt{50}=-3\sqrt{2}$ |
9.我国药学家屠呦呦荣获2015年诺贝尔医学奖,其突出贡献是在东晋葛洪《肘后备急方•治寒热诸症方》的启发下.创制了新型抗疟药一青蒿素.她获得的奖金为400万瑞典克朗,约合300万人民币.“300万”可用科学记数法表示为( )
| A. | 3×107 | B. | 0.3×107 | C. | 3×106 | D. | 30×105 |
16.已知一次函数y=kx+b-x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )
| A. | k>1,b<0 | B. | k>1,b>0 | C. | k>0,b>0 | D. | k>0,b<0 |
14.省政府提出2016年要实现180 000农村贫困人口脱贫,数据180 000用科学记数法表示为( )
| A. | 1.8×103 | B. | 1.8×104 | C. | 1.8×105 | D. | 1.8×106 |
 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,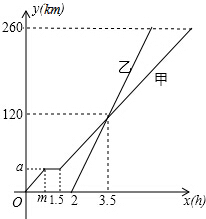 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论: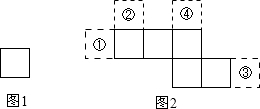
 如图中的四边形均为矩形,根据图形,写出一个正确的等式am+bm+cm=m(a+b+c).
如图中的四边形均为矩形,根据图形,写出一个正确的等式am+bm+cm=m(a+b+c).