题目内容
13．命题甲：由正比例函数图象上任意一点的坐标可以确定该正比例函数的解析式；命题乙：大边上的中线等于大边一半的三角形是直角三角形．
则下列判断正确的是（ ）
| A． | 两命题都正确 | B． | 两命题都不正确 | C． | 甲不正确乙正确 | D． | 甲正确乙不正确 |
分析 分别判断两个命题后即可确定正确的选项．
解答 解：命题甲：由正比例函数图象上任意一点（除原点外）的坐标可以确定该正比例函数的解析式，不正确；
命题乙：大边上的中线等于大边一半的三角形是直角三角形，正确，
故选C．
点评 本题考查了命题与定理的知识，解题的关键是能够了解正比例函数的解析式的求法及直角三角形的判定等知识．
练习册系列答案
相关题目
4．
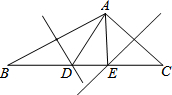如图，△ABC中，∠BAC＞90°，其中AB、AC的垂直平分线交BC于点D、E，△ADE的周长为16，则BC的长（ ）
如图，△ABC中，∠BAC＞90°，其中AB、AC的垂直平分线交BC于点D、E，△ADE的周长为16，则BC的长（ ）| A． | 16 | B． | 18 | C． | 24 | D． | 32 |
1．在函数y=$\sqrt{2+x}$中，自变量x的取值范围是（ ）
| A． | x≥-2 | B． | x≤-2 | C． | x＞-2 | D． | x＜-2 |
8．下列等式一定成立的是（ ）
| A． | $\sqrt{5}-\sqrt{2}=\sqrt{3}$ | B． | $\frac{{\sqrt{7}}}{{\sqrt{5}}}=\sqrt{\frac{7}{5}}$ | C． | $\sqrt{x^2}=\sqrt{x}•\sqrt{x}$ | D． | $\sqrt{{{（π-4）}^2}}$=π-4 |
18．（x3）2的计算结果是（ ）
| A． | x9 | B． | x6 | C． | x5 | D． | x |
2．若顺次连结四边形ABCD各边中点所得四边形是矩形，则四边形ABCD必定是（ ）
| A． | 菱形 | B． | 对角线相互垂直的四边形 | ||
| C． | 正方形 | D． | 对角线相等的四边形 |
3．下列图形中，既是中心对称图形又是轴对称图形的是（ ）
| A． |  | B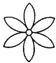． |  | C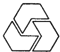． |  | D． |  |