题目内容
4.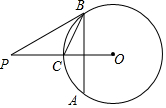 如图,已知P是⊙O外一点,PO交⊙O于点C,CO=CP=4,弦AB垂直平分OC.
如图,已知P是⊙O外一点,PO交⊙O于点C,CO=CP=4,弦AB垂直平分OC.(1)求BC的长;
(2)求证:PB是⊙O的切线.
分析 (1)由OA=OB,弦AB⊥OC,易证得△OBC是等边三角形,则可求得BC的长;
(2)由OC=CP=2,△OBC是等边三角形,可求得BC=CP,即可得∠P=∠CBP,又由等边三角形的性质,∠OBC=60°,∠CBP=30°,则可证得OB⊥BP,继而证得PB是⊙O的切线.
解答 (1)解:∵弦AB垂直平分OC,
∴BCBO,
∵OB=OC,
∴OB=BC=CO,
∴△OBC是等边三角形,
∴BC=OC=2;
(2)证明:∵OC=CP,BC=OC,
∴BC=CP,
∴∠CBP=∠CPB,
∵△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠CBP=30°,
∴∠OBP=∠CBP+∠OBC=90°,
∴OB⊥BP,
∵点B在⊙O上,
∴PB是⊙O的切线.
点评 本题考查了切线的判定,等边三角形的判定与性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
14.某同学骑车从学校到家,每分行1.5千米,某天回家时,速度提高到每分行2千米,结果提前5分回家,设原来从学校到家之间骑车用x分,则列方程为( )
| A. | 1.5x=2(x+5) | B. | 1.5x=2(x-5) | C. | 1.5(x+5)=2x | D. | 1.5(x-5)=2x |
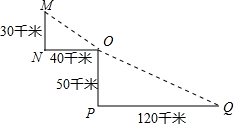 如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速的建设成本是100万元∕千米,该沿江高速的造价是多少?
如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速的建设成本是100万元∕千米,该沿江高速的造价是多少?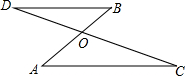 如图.BD∥AC,AB与CD相交于点O,已知△OBD∽△OAC,$\frac{OD}{OC}$=$\frac{2}{3}$,OB=2,求AB的长.
如图.BD∥AC,AB与CD相交于点O,已知△OBD∽△OAC,$\frac{OD}{OC}$=$\frac{2}{3}$,OB=2,求AB的长.