题目内容
4.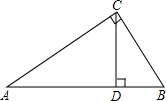 △ABC中,∠C=90°,BC=3,AB=5,CD⊥AB于D,
△ABC中,∠C=90°,BC=3,AB=5,CD⊥AB于D,(1)求AC长;
(2)求CD长.
分析 (1)直接根据勾股定理即可得出结论;
(2)根据三角形的面积公式即可得出结论.
解答 解:(1)∵△ABC中,∠C=90°,BC=3,AB=5,
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4;
(2)∵CD⊥AB,AB=5,由(1)知AC=4,
∴AB•CD=AC•BC,即CD=$\frac{AC•BC}{AB}$=$\frac{4×3}{5}$=$\frac{12}{5}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若x+y=7,xy=-8,下列各式计算结果不正确的是( )
| A. | (x+y)2=49 | B. | x2+y2=65 | C. | (x-y)2=81 | D. | (xy)2=-64 |
13.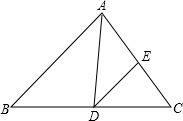 如图,在△ABC中,∠B=46°,∠ADE=40°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠C的大小是( )
如图,在△ABC中,∠B=46°,∠ADE=40°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠C的大小是( )
 如图,在△ABC中,∠B=46°,∠ADE=40°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠C的大小是( )
如图,在△ABC中,∠B=46°,∠ADE=40°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠C的大小是( )| A. | 46° | B. | 66° | C. | 54° | D. | 80° |
14.从下列4个命题中任取一个 ①6的平方根是$\sqrt{6}$; ②$\sqrt{6}$是方程x2-6=0的解; ③如果两个图形是位似图形,则这两个图形一定相似.④在半径为4的圆中,15°的圆周角所对的弧长为$\frac{2}{3}$π;是真命题的概率是( )
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
 如图,已知AC平分∠DAB,∠1=∠2.∠B=60°,求∠BCD的度数?
如图,已知AC平分∠DAB,∠1=∠2.∠B=60°,求∠BCD的度数?