题目内容
12. 如图,已知AC平分∠DAB,∠1=∠2.∠B=60°,求∠BCD的度数?
如图,已知AC平分∠DAB,∠1=∠2.∠B=60°,求∠BCD的度数?
分析 由条件可证明∠2=∠CAB,可证明AB∥CD,再根据平行线的性质可求得∠BCD.
解答 解:
∵AC平分∠DAB,
∴∠1=∠BAC,
又∠1=∠2,
∴∠2=∠BAC,
∴AB∥CD,
∴∠B+∠BCD=180°,
∴∠BCD=180°-∠B=180°-60°=120°,
即∠BCD的度数为120°.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.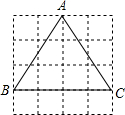 正方形网格中,△ABC如图放置,则sin∠BAC=( )
正方形网格中,△ABC如图放置,则sin∠BAC=( )
 正方形网格中,△ABC如图放置,则sin∠BAC=( )
正方形网格中,△ABC如图放置,则sin∠BAC=( )| A. | $\frac{2}{{\sqrt{13}}}$ | B. | $\frac{3}{{\sqrt{13}}}$ | C. | $\frac{4}{{\sqrt{13}}}$ | D. | $\frac{12}{13}$ |
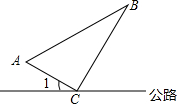 如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近?
如图,在公路的同侧有A、B两个送奶站,C为公路上一个供奶站,CA和CB为供奶站路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边行走,速度为2.5km/h,问多长时间后这人距离B送奶站最近?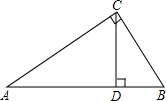 △ABC中,∠C=90°,BC=3,AB=5,CD⊥AB于D,
△ABC中,∠C=90°,BC=3,AB=5,CD⊥AB于D,