题目内容
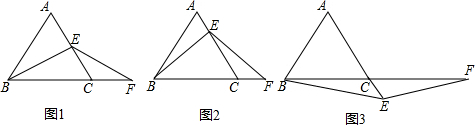
已知△ABC是等边三角形,E是AC边上一点,F是BC边延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,若E是AC边的中点,猜想BE与EF的数量关系为 .
(2)如图2,若E是线段AC上的任意一点,其它条件不变,上述线段BE、EF的数量关系是否发生变化,写出你的猜想并加以证明.
(3)如图3,若E是线段AC延长线上的任意一点,其它条件不变,上述线段BE、EF的数量关系是否发生变化,写出你的猜想并加以证明.
(1)如图1,若E是AC边的中点,猜想BE与EF的数量关系为
(2)如图2,若E是线段AC上的任意一点,其它条件不变,上述线段BE、EF的数量关系是否发生变化,写出你的猜想并加以证明.
(3)如图3,若E是线段AC延长线上的任意一点,其它条件不变,上述线段BE、EF的数量关系是否发生变化,写出你的猜想并加以证明.

考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等腰三角形三线合一的性质可得∠CBE=
∠ABC=30°,AE=CE,所以CE=CF,然后等边对等角的性质可得∠F=∠CEF,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠F=30°,从而得到∠CBE=∠F,根据等角对等边的性质即可证明;
(2)图2,过点E作EG∥BC,交AB于点G,根据菱形的性质结合∠ABC=60°可得△ABC是等边三角形,然后根据等边三角形的性质得到AB=AC,∠ACB=60°,再求出△AGE是等边三角形,根据等边三角形的性质得到AG=AE,从而可以求出BG=CE,再根据等角的补角相等求出∠BGE=∠ECF=120°,然后利用“边角边”证明△BGE和△ECF 全等,根据全等三角形对应边相等即可得证;
(3)图3,证明思路与方法与图2完全相同.
| 1 |
| 2 |
(2)图2,过点E作EG∥BC,交AB于点G,根据菱形的性质结合∠ABC=60°可得△ABC是等边三角形,然后根据等边三角形的性质得到AB=AC,∠ACB=60°,再求出△AGE是等边三角形,根据等边三角形的性质得到AG=AE,从而可以求出BG=CE,再根据等角的补角相等求出∠BGE=∠ECF=120°,然后利用“边角边”证明△BGE和△ECF 全等,根据全等三角形对应边相等即可得证;
(3)图3,证明思路与方法与图2完全相同.
解答: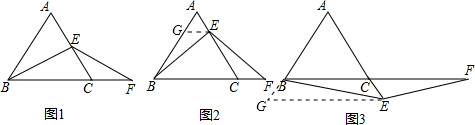 (1)答:猜想BE与EF的数量关系为:BE=EF;
(1)答:猜想BE与EF的数量关系为:BE=EF;
证明:(1)∵△ABC是等边三角形,E是线段AC的中点,
∴∠CBE=
∠ABC=30°,AE=CE,
∵AE=CF,
∴CE=CF,
∴∠F=∠CEF,
∵∠F+∠CEF=∠ACB=60°,
∴∠F=30°,
∴∠CBE=∠F,
∴BE=EF;
(2)答:猜想BE=EF.
证明如下:如图2,过点E作EG∥BC,交AB于点G,
∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
在△BGE与△ECF中,
,
∴△BGE≌△ECF(SAS),
∴BE=EF;
(3)BE=EF.
证明如下:如图3,过点E作EG∥BC交AB延长线于点G,
∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
又∵∠BGE=∠ECF=60°,
∴在△BGE与△ECF中,
,
∴△BGE≌△ECF(SAS),
∴BE=EF.
 (1)答:猜想BE与EF的数量关系为:BE=EF;
(1)答:猜想BE与EF的数量关系为:BE=EF;证明:(1)∵△ABC是等边三角形,E是线段AC的中点,
∴∠CBE=
| 1 |
| 2 |
∵AE=CF,
∴CE=CF,
∴∠F=∠CEF,
∵∠F+∠CEF=∠ACB=60°,
∴∠F=30°,
∴∠CBE=∠F,
∴BE=EF;
(2)答:猜想BE=EF.
证明如下:如图2,过点E作EG∥BC,交AB于点G,
∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
在△BGE与△ECF中,
|
∴△BGE≌△ECF(SAS),
∴BE=EF;
(3)BE=EF.
证明如下:如图3,过点E作EG∥BC交AB延长线于点G,
∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE,
∴BG=CE,
又∵CF=AE,
∴GE=CF,
又∵∠BGE=∠ECF=60°,
∴在△BGE与△ECF中,
|
∴△BGE≌△ECF(SAS),
∴BE=EF.
点评:本题考查了等边三角形的判定与性质,全等三角形的判定与性质,作出辅助线,利用等边三角形的性质找出全等的条件是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 如图,BD是矩形ABCD的一条对角线.
如图,BD是矩形ABCD的一条对角线. 如图,已知在△ABC中,AD平分∠EAC且AD∥BC,那么∠B=∠C吗?请说明理由.
如图,已知在△ABC中,AD平分∠EAC且AD∥BC,那么∠B=∠C吗?请说明理由. 请在括号里补充完整下面证明过程:
请在括号里补充完整下面证明过程: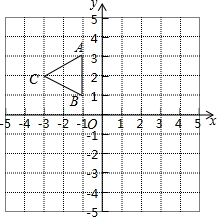 如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2),以原点O为位似中心,将△ABC放大为原来的2倍得到△A1B1C1,请在第四象限内画出△A1B1C1,并写出A1、B1、C1三点的坐标.
如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2),以原点O为位似中心,将△ABC放大为原来的2倍得到△A1B1C1,请在第四象限内画出△A1B1C1,并写出A1、B1、C1三点的坐标.