题目内容
 请在括号里补充完整下面证明过程:
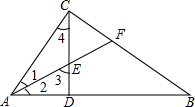
请在括号里补充完整下面证明过程:已知:如图,△ABC中,∠ACB=90°,AF平分∠CAB,交CD于点E,交CB于点F,且∠CEF=∠CFE.求证:CD⊥AB.
证明:∵AF平分∠CAB,
∴∠1=∠2(
∵∠CEF=∠CFE,∠3=∠CEF
∴∠CFE=∠3(
∵∠CFE=∠2+∠B,∠3=∠4+∠1(
∴∠2+∠B=∠4+∠1
∵∠1=∠2
∴(
∵∠ACB=90°∴∠CAB+∠B=90°∴∠CAB+∠4=90°
∴(
∴CD⊥AB(
考点:三角形的外角性质
专题:推理填空题
分析:首先根据角平分线定义可得∠1=∠2,然后再利用等量代换可得∠CFE=∠3,根据三角形外角的性质得到∠2+∠B=∠4+∠1,进而可得∠B=∠4,再根据角的和差关系可得∠CAB+∠4=90°,进而得到CD⊥AB.
解答: 证明:∵AF平分∠CAB,
证明:∵AF平分∠CAB,
∴∠1=∠2( 角平分线的定义),
∵∠CEF=∠CFE,∠3=∠CEF,
∴∠CFE=∠3( 等量代换),
∵∠CFE=∠2+∠B,∠3=∠4+∠1( 三角形的一个外角等于与它不相邻的两个内角的和),
∴∠2+∠B=∠4+∠1,
∵∠1=∠2,
∴(∠B=∠4)( 等式的基本性质)
∵∠ACB=90°,
∴∠CAB+∠B=90°,
∴∠CAB+∠4=90°
∴(∠ADC=90°)
∴CD⊥AB( 垂直的定义).
故答案为:角平分线的定义;等量代换;三角形的一个外角等于与它不相邻的两个内角的和;∠B=∠4;等式的基本性质;∠ADC=90°.
 证明:∵AF平分∠CAB,
证明:∵AF平分∠CAB,∴∠1=∠2( 角平分线的定义),
∵∠CEF=∠CFE,∠3=∠CEF,
∴∠CFE=∠3( 等量代换),
∵∠CFE=∠2+∠B,∠3=∠4+∠1( 三角形的一个外角等于与它不相邻的两个内角的和),
∴∠2+∠B=∠4+∠1,
∵∠1=∠2,
∴(∠B=∠4)( 等式的基本性质)
∵∠ACB=90°,
∴∠CAB+∠B=90°,
∴∠CAB+∠4=90°
∴(∠ADC=90°)
∴CD⊥AB( 垂直的定义).
故答案为:角平分线的定义;等量代换;三角形的一个外角等于与它不相邻的两个内角的和;∠B=∠4;等式的基本性质;∠ADC=90°.
点评:此题主要考查了三角形内角与外角的关系,以及垂直定义和角平分线定义,关键是理清角之间的关系.

练习册系列答案
相关题目
已知一组数据:1,2,6,3,3,下列说法正确的是( )
| A、众数是3 | B、中位数是6 |
| C、平均数是4 | D、方差是5 |
 将一副三角尺如图叠放在一起,求
将一副三角尺如图叠放在一起,求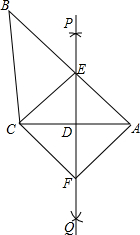 如图,已知△ABC,按如下步骤作图:
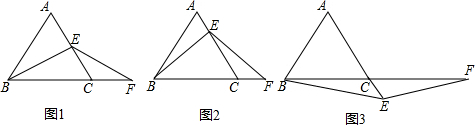
如图,已知△ABC,按如下步骤作图: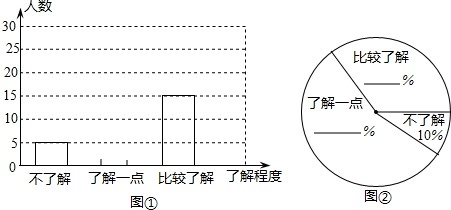
 如图,矩形ABCD在平面直角坐标系的位置如图,A(0,0)、B(6,0)、D(0,4).
如图,矩形ABCD在平面直角坐标系的位置如图,A(0,0)、B(6,0)、D(0,4).