题目内容
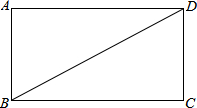 如图,BD是矩形ABCD的一条对角线.
如图,BD是矩形ABCD的一条对角线.(1)作BD的垂直平分线EF,分别交AD、BC于点E、F,垂足为点O.(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)求证:DE=BF.
考点:作图—基本作图,线段垂直平分线的性质,矩形的性质
专题:作图题,证明题
分析:(1)分别以B、D为圆心,以大于
BD的长为半径四弧交于两点,过两点作直线即可得到线段BD的垂直平分线;
(2)利用垂直平分线证得△DEO≌△BFO即可证得结论.
| 1 |
| 2 |
(2)利用垂直平分线证得△DEO≌△BFO即可证得结论.
解答:解:(1)答题如图:

(2)∵四边形ABCD为矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵EF垂直平分线段BD,
∴BO=DO,
在△DEO和三角形BFO中,
,
∴△DEO≌△BFO(ASA),
∴DE=BF.

(2)∵四边形ABCD为矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵EF垂直平分线段BD,
∴BO=DO,
在△DEO和三角形BFO中,
|
∴△DEO≌△BFO(ASA),
∴DE=BF.
点评:本题考查了基本作图及全等三角形的判定与性质,了解基本作图是解答本题的关键,难度中等.

练习册系列答案
相关题目
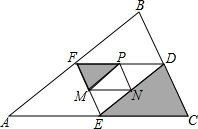 如图,△ABC三边的中点D,E,F组成△DEF,△DEF三边的中点M,N,P组成△MNP,将△FPM与△ECD涂成阴影.假设可以随意在△ABC中取点,那么这个点取在阴影部分的概率为
如图,△ABC三边的中点D,E,F组成△DEF,△DEF三边的中点M,N,P组成△MNP,将△FPM与△ECD涂成阴影.假设可以随意在△ABC中取点,那么这个点取在阴影部分的概率为 将一副三角尺如图叠放在一起,求
将一副三角尺如图叠放在一起,求 如图,已知点是直线AB上一点,射线OD、OE分别是∠BOC、∠AOC的平分线.
如图,已知点是直线AB上一点,射线OD、OE分别是∠BOC、∠AOC的平分线.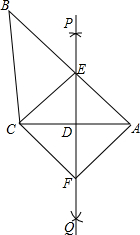 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图: