题目内容
20.先化简,再求值:$\frac{a+2b}{a+b}+\frac{{2{b^2}}}{{{a^2}-{b^2}}}$,其中a=-2,b=$\frac{1}{4}$.分析 先根据分式混合运算的法则把原式进行化简,再把a,b的值代入进行计算即可.
解答 解:原式=$\frac{{(a+2b)({a-b})+2{b^2}}}{{{a^2}-{b^2}}}$
=$\frac{{{a^2}-ab+2ab-2{b^2}+2{b^2}}}{{{a^2}-{b^2}}}$
=$\frac{a}{a-b}$.
当a=-2,b=$\frac{1}{4}$时,
原式=$\frac{-2}{-2-\frac{1}{4}}$=$\frac{8}{9}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
11.若式子$\sqrt{x-7}$在实数范围内有意义,则x的取值范围是( )
| A. | x<7 | B. | x≤7 | C. | x>7 | D. | x≥7 |
5.若(xny•xym)5=x10y15,则3m(n+1)=( )
| A. | 12 | B. | 10 | C. | 8 | D. | 15 |
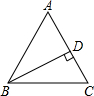 如图,在△ABC中,AB=AC,BD⊥AC于D,BD=4,CB=5,求AB的长.
如图,在△ABC中,AB=AC,BD⊥AC于D,BD=4,CB=5,求AB的长. 如图,已知BE是∠ABC的角平分线,∠1=∠3,你能从图中找到平行的线段吗?请说明理由.
如图,已知BE是∠ABC的角平分线,∠1=∠3,你能从图中找到平行的线段吗?请说明理由.