题目内容
15.抛物线y=2x2-2$\sqrt{2}$x+1与坐标轴的交点个数是2.分析 当x=0时,求出与y轴的纵坐标;当y=0时,求出关于x的一元二次方程2x2-2$\sqrt{2}$x+1的根的判别式的符号,从而确定该方程的根的个数,即抛物线y=2x2-2$\sqrt{2}$x+1与x轴的交点个数.
解答 解:当x=0时,y=1,
则与y轴的交点坐标为(0,1),
当y=0时,2x2-2$\sqrt{2}$x+1=0,
△=(2$\sqrt{2}$)2-4×1×2=0,
所以,该方程有两个相等解,即抛物线y=2x2-2$\sqrt{2}$x+1与x轴有一个点.
综上所述,抛物线y=2x2-2$\sqrt{2}$x+1与坐标轴的交点个数是2个.
故答案为:2.
点评 本题考查了抛物线与坐标轴的交点,分别令x=0,y=0,将抛物线转化为方程是解题的关键.

练习册系列答案
相关题目
6.抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )
| A. | y=-2x2+8x+3 | B. | y=-2x2-8x+3 | C. | y=-2x2+8x-5 | D. | y=-2x2-8x+2 |
20.在等边△ABC内部任取一点P,将△ABP绕点A旋转到△ACQ,则△APQ为( )
| A. | 不等腰的直角三角形 | B. | 腰和底不等的等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等边三角形 |
7.将抛物线y=x2-2向左平移1个单位后再向上平移1个单位所得抛物线的表达式为( )
| A. | y=(x-1)2-1 | B. | y=(x+1)2-1 | C. | y=(x+1)2+1 | D. | y=(x-1)2+1 |
4.洪峰到来前,120名战士奉命加固堤坝,已知5人运沙袋3人堆垒沙袋,正好运来的沙袋能及时用上且不窝工,为了合理安排,如果设x人运送沙袋,其余人堆垒沙袋,那么以下所列方程正确的是( )
| A. | $\frac{120-x}{2}$=x | B. | 120-x=$\frac{5}{3}$x | C. | x=$\frac{5}{3}$(120-x) | D. | 3x+2x=120 |
 如图,在Rt△ABC中,∠B=90°
如图,在Rt△ABC中,∠B=90°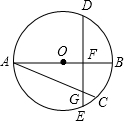 如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G.
如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G.