题目内容
10.我们已经学习了一元二次方程的四种解法:因式分解法、直接开平方怯、配方法和公式法.请选择适当的方法解下列方程.(1)x2-3x+1=0;
(2)(x-1)2=3;
(3)x2+2x+1=0;
(4)x2-2x=4.
分析 (1)求出b2-4ac的值,再代入公式求出即可;
(2)两边开方,即可得出两个一元一次方程,求出方程的解即可;
(3)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(4)配方,开方,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)x2-3x+1=0,
∵a=1,b=-3,c=1,b2-4ac=(-3)2-4×1×1=5,
∴x=$\frac{3±\sqrt{5}}{2}$,
∴x1=$\frac{3+\sqrt{5}}{2}$,x2=$\frac{3-\sqrt{5}}{2}$;
(2)(x-1)2=3,
开方得:x-1=±$\sqrt{3}$,
x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$;
(3)x2+2x+1=0,
(x+1)2=0,
∴x1=x2=-1;
(4)x2-2x=4,
x2-2x+1=4+1,
(x-1)2=5,
x-1=$±\sqrt{5}$,
x1=1+$\sqrt{5}$,x2=1-$\sqrt{5}$.
点评 本题考查了解一元二次方程,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列实数中,无理数是( )
| A. | -$\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{9}$ | D. | -|-5| |
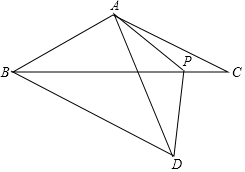 如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4.
如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4. △ABC中,作BD⊥AC于D,CE⊥AB于E,连DE,若∠ABC=45°,求∠EDB的度数?
△ABC中,作BD⊥AC于D,CE⊥AB于E,连DE,若∠ABC=45°,求∠EDB的度数?