题目内容
14.已知k是方程x2-101x+1=0的一个不为0的根,不解方程,你能求出k2-100k+$\frac{101}{{k}^{2}+1}$的值吗?如果能,请写出解答过程;如果不能,请说明理由.(用方程根的定义解答)分析 利用一元二次方程解得定义得到k2=101k-1,利用代入法得到原式=101k-1-100k+$\frac{101}{101k-1+1}$,化简后得到原式=k-1+$\frac{1}{k}$,然后通分后再利用整体代入的方法计算.
解答 解:能.
∵k是方程x2-101x+1=0的一个不为0的根,
∴k2-101k+1=0,
即k2=101k-1,
∴k2-100k+$\frac{101}{{k}^{2}+1}$=101k-1-100k+$\frac{101}{101k-1+1}$
=k-1+$\frac{1}{k}$
=$\frac{{k}^{2}+1}{k}$-1
=$\frac{101k-1+1}{k}$-1
=101-1
=100.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列运算正确的是( )
| A. | a+a2=a3 | B. | (a2)3=a6 | C. | (x-y)2=x2-y2 | D. | a2a3=a6 |
5.下列实数中,无理数是( )
| A. | -$\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{9}$ | D. | -|-5| |
10.将抛物线y=3x2向上平移3个单位,再向右平移2个单位,那么得到的抛物线的解析式为( )
| A. | y=3(x+2)2+3 | B. | y=3(x-2)2+3 | C. | y=3(x+2)2-3 | D. | y=3(x-2)2-3 |
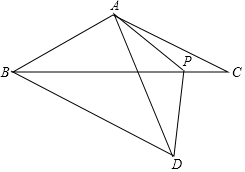 如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4.
如图,在等腰△ABC中,AB=AC,点P为底边BC上一点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC=120°,连接BD,AB=4.