题目内容
15.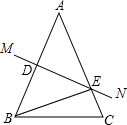 在△ABC中,AB=AC=14cm,D为BA的中点,DE⊥AB交BC于E.若△EBC的周长为25cm,则BC长为11cm.
在△ABC中,AB=AC=14cm,D为BA的中点,DE⊥AB交BC于E.若△EBC的周长为25cm,则BC长为11cm.
分析 先根据垂直平分线的性质判定AE=BE;然后再找出AB、AC、AE间的数量关系;最后将其代入△EBC的周长公式求解即可.
解答 解:在△ABE中,
∵D是AB的中点,DE⊥AB于D交AC于E,
∴AE=BE;
在△ABC中,
∵AB=AC=14cm,AC=AE+EC,
又∵CE+BE+BC=24cm,
∴BC=11cm.
故答案为:11.
点评 此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.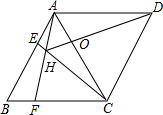 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
4.已知等腰三角形的两边长是5cm和6cm,则此三角形的周长是( )
| A. | 16cm | B. | 17cm | C. | 11cm | D. | 16cm或17cm |
 如图所示,D是△ABC的边AB上一点,∠B=∠1,BD=4,AD=3,则AC=$\sqrt{21}$.
如图所示,D是△ABC的边AB上一点,∠B=∠1,BD=4,AD=3,则AC=$\sqrt{21}$. 如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,且∠1=∠2.求证:四边形ABCD是矩形.
如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,且∠1=∠2.求证:四边形ABCD是矩形.