题目内容
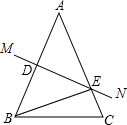
20. 如图所示,D是△ABC的边AB上一点,∠B=∠1,BD=4,AD=3,则AC=$\sqrt{21}$.
如图所示,D是△ABC的边AB上一点,∠B=∠1,BD=4,AD=3,则AC=$\sqrt{21}$.
分析 首先证明△ADC∽△ACB,然后由相似三角形的性质可知:$\frac{AC}{AB}=\frac{AD}{AC}$,即$\frac{AC}{7}=\frac{3}{AC}$,从而可求得解得:AC=$\sqrt{21}$.
解答 解:∵BD=4,AD=3,
∴AB=7.
∵∠B=∠1,∠A=∠A,
∴△ADC∽△ACB.
∴$\frac{AC}{AB}=\frac{AD}{AC}$,即$\frac{AC}{7}=\frac{3}{AC}$.
解得:AC=$\sqrt{21}$或AC=-$\sqrt{21}$(舍去).
故答案为:$\sqrt{21}$.
点评 本题主要考查的是相似三角形的性质和判定,熟练掌握相似三角形的性质和判定是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
12.在?ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,请判断下列结论:其中错误的结论是( )
| A. | BE=DF | B. | AG=GH=HC | C. | EG=$\frac{1}{2}$BG | D. | S△ABE=2S△AGE |
9.下列调查中,适合作全面调查的是( )
| A. | 了解海尔牌电冰箱的市场占有率 | B. | 了解奇瑞牌汽车每百里的耗油量 | ||
| C. | 了解某班级参加课外小组的人数 | D. | 了解某种药品的疗效 |
 在△ABC中,AB=AC=14cm,D为BA的中点,DE⊥AB交BC于E.若△EBC的周长为25cm,则BC长为11cm.
在△ABC中,AB=AC=14cm,D为BA的中点,DE⊥AB交BC于E.若△EBC的周长为25cm,则BC长为11cm.