题目内容
20.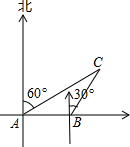 如图所示,某船以每小时40海里的速度向正东方向航行,在点A测得岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛C在北偏东30方向上,已知该岛周围18海里内有暗礁.
如图所示,某船以每小时40海里的速度向正东方向航行,在点A测得岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛C在北偏东30方向上,已知该岛周围18海里内有暗礁.(1)试说明点B是否在暗礁区域外?
(2)若继续向东航行有无触礁危险?请说明理由.
分析 (1)过点C作CM⊥AB于M,设CM=x,根据题意和特殊角的三角函数值求出AM和BM的值,从而求出x的值,再与18海里进行比较即可得出答案.
(2)根据(1)求出CM的值,再与18进行比较,即可得出答案.
解答  解:(1)过点C作CM⊥AB于M,设CM=x,
解:(1)过点C作CM⊥AB于M,设CM=x,
∵∠CAM=30°∠CBM=60°,
∴AM=$\sqrt{3}$x,BC=$\frac{2\sqrt{3}}{3}$x,BM=$\frac{\sqrt{3}}{3}$x,
由题意知:$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=$\frac{1}{2}$×40,即$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=20,
解得:x=10$\sqrt{3}$(海里),
∴BC=$\frac{2\sqrt{3}}{3}$×10$\sqrt{3}$=20>18,
∴点B在暗礁区域之外;
(2)由(1)知:CM=x=10$\sqrt{3}$≈17.32<18,
故继续向东航行有触礁的危险.
点评 此题考查了解直角三角形的应用,用到的知识点是特殊角的三角函数值、方向角问题,关键是根据题意作出辅助线,构造直角三角形.

练习册系列答案
相关题目
8.已知B、C两点把线段AD分成2:3:4三部分,M是AD的中点,CD=12,则MC的长为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
15.长度单位1纳米=10-9米,一种新型病毒直径为3100纳米,用科学记数法表示该病毒直径是( )米.
| A. | 31×10-6 | B. | 0.31×10-5 | C. | 3.1×10-6 | D. | 3.1×10-5 |
10.下列运算正确的是( )
| A. | (-4m2)3=-4m6 | B. | ${(-\frac{1}{2})^{-4}}+{(π-3)^0}$=16 | ||
| C. | (a+b)2=(a-b)2+4ab | D. | $9{x^3}{y^2}÷(-\frac{1}{3}{x^3}y)=-3y$ |