题目内容
18.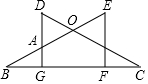 如图,DG⊥BC于G,EF⊥BC于F,连结CD,BE,且CD=BE,DG=EF.
如图,DG⊥BC于G,EF⊥BC于F,连结CD,BE,且CD=BE,DG=EF.(1)求证:△DGC≌△EFB;
(2)求证:△OBC为等腰三角形.
分析 (1)根据HL即可证明.
(2)利用全等三角形的性质,可知∠EBF=∠DCG,由此推出OB=OC即可.
解答 证明:(1)∵DG⊥BC于G,EF⊥BC于F
∴∠DGC=∠EFB=90°
在Rt△DGC和Rt△EFB中,
$\left\{\begin{array}{l}{DG=EF}\\{CD=BE}\end{array}\right.$
∴Rt△DGC≌Rt△EFB(HL),
(2)∵△DGC≌△EFB
∴∠EBF=∠DCG
∴OB=OC
∴△OBC为等腰三角形
点评 本题考查全等三角形的判定和性质,解题的关键是熟练掌握全等三角形的判定和性质,属于基础题.

练习册系列答案
相关题目
3.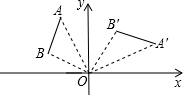 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )| A. | (2,5) | B. | (5,2) | C. | (4,$\frac{5}{2}$) | D. | ($\frac{5}{2}$,4) |
7. 将连续的奇数1,3,5,7,9,…排成如图所示的数表,若阴影十字框上下左右移动,则阴影十字框中的五个数字之和可以是( )
将连续的奇数1,3,5,7,9,…排成如图所示的数表,若阴影十字框上下左右移动,则阴影十字框中的五个数字之和可以是( )
 将连续的奇数1,3,5,7,9,…排成如图所示的数表,若阴影十字框上下左右移动,则阴影十字框中的五个数字之和可以是( )
将连续的奇数1,3,5,7,9,…排成如图所示的数表,若阴影十字框上下左右移动,则阴影十字框中的五个数字之和可以是( )| A. | 2025 | B. | 2020 | C. | 2017 | D. | 2018 |
8. 在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作PQ∥BC,交AB于点P,交AC于点Q,若∠A=60°,则∠PEB+∠QEC=( )
在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作PQ∥BC,交AB于点P,交AC于点Q,若∠A=60°,则∠PEB+∠QEC=( )
 在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作PQ∥BC,交AB于点P,交AC于点Q,若∠A=60°,则∠PEB+∠QEC=( )
在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作PQ∥BC,交AB于点P,交AC于点Q,若∠A=60°,则∠PEB+∠QEC=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
 如图,在直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-4,1)、B(-1,1)、C(-4,3).
如图,在直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-4,1)、B(-1,1)、C(-4,3).