题目内容

2．若y=$\sqrt{x-\frac{1}{2}}$+$\sqrt{\frac{1}{2}-x}$-6，则xy=-3．

分析 根据分式有意义的条件即可求出x与y的值．

解答 解：由题意可知：$\left\{\begin{array}{l}{x-\frac{1}{2}≥0}\\{\frac{1}{2}-x≥0}\end{array}\right.$，
解得：x=$\frac{1}{2}$，
∴y=0+0-6=-6，
∴xy=-3，
故答案为：-3

点评 本题考查二次根式有意义的条件，解题的关键是正确理解二次根式有意义的条件，本题属于基础题型．

练习册系列答案
相关题目
12．（1）解方程：$\frac{2}{x}$-$\frac{1}{x+1}$=0；
（2）解不等式组：$\left\{\begin{array}{l}{x+3＞0}\\{1-2x≤-3}\end{array}\right.$．
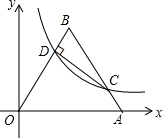13．如图，正三角形△OAB的边OA在x轴上，D是OB边上的动点（不与端点O，B重合），双曲线y=$\frac{k}{x}$过点D，且与BA交于点C，设AB=8，$\frac{BD}{BO}$=n．
（1）当n=$\frac{1}{4}$时，求反比例函数的表达式；
（2）若DC⊥BD，求n的值．
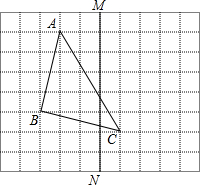10．如图，在正方形网格上有一个△ABC．
（1）画出△ABC关于直线MN的对称图形（不写画法）；
（2）若网格上的每个小正方形的边长为1，则△ABC的面积为$\frac{17}{2}$．
17．风电已成为我国继煤电、水电之后的第三大电源，风电机组主要由塔杆和叶片组成（如图1），图2是从图1引出的平面图．假设你站在A处测得塔杆顶端C的仰角是55°，沿HA方向水平前进43米到达山底G处，在山顶B处发现正好一叶片到达最高位置，此时测得叶片的顶端D（D、C、H在同一直线上）的仰角是45°．已知叶片的长度为35米（塔杆与叶片连接处的长度忽略不计），山高BG为10米，BG⊥HG，CH⊥AH，求塔杆CH的高．（参考数据：tan55°≈1.4，tan35°≈0.7，sin55°≈0.8，sin35°≈0.6）
7．如图，在△ABC中，∠ACB=90°，CD是中线，AC=BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E，F，DF与AC交于点M，DE与BC交于点N．

（1）如图1，若CE=CF，求证：DE=DF；
（2）如图2，在∠EDF绕点D旋转的过程中：
①探究三条线段AB，CE，CF之间的数量关系，并说明理由；
②若CE=4，CF=2，求DN的长．
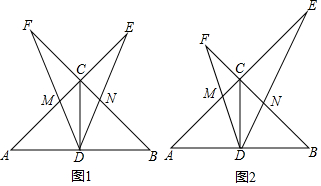
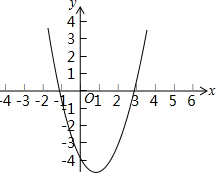14．设a、b是任意两个实数，用max{a，b}表示a、b两数中较大者，例如：max{-1，-1}=-1，max{1，2}=2，max{4，3}=4，参照上面的材料，解答下列问题：
（1）max{5，2}=5，max{0，3}=3；
（2）若max{3x+1，-x+1}=-x+1，求x的取值范围；
（3）求函数y=x2-2x-4与y=-x+2的图象的交点坐标，函数y=x2-2x-4的图象如图所示，请你在图中作出函数y=-x+2的图象，并根据图象直接写出max{-x+2，x2-2x-4}的最小值．
11．在平面直角坐标系中，点P（m-3，4-2m）不可能在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
12．计算：-（-2）+$\sqrt{8}$-2sin45°+（-1）3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网