题目内容
2.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,若把第一个三角形数记为x1,第二个三角形数记为x2,…第n个三角形数记为xn,则xn+xn+1=(n+1)2.分析 根据三角形数得到x1=1,x2=3=1+2,x3=6=1+2+3,x4=10=1+2+3+4,x5=15=1+2+3+4+5,即三角形数为从1到它的顺号数之间所有整数的和,即xn=1+2+3+…+n=$\frac{n(n+1)}{2}$、xn+1=$\frac{(n+1)(n+2)}{2}$,然后计算xn+xn+1可得.
解答 解:∵x1=1,
x2═3=1+2,
x3=6=1+2+3,
x4═10=1+2+3+4,
x5═15=1+2+3+4+5,
…
∴xn=1+2+3+…+n=$\frac{n(n+1)}{2}$,xn+1=$\frac{(n+1)(n+2)}{2}$,
则xn+xn+1=$\frac{n(n+1)}{2}$+$\frac{(n+1)(n+2)}{2}$=(n+1)2,
故答案为:(n+1)2.
点评 本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
17.若x2+4x-4=0,则3(x-2)2-6(x+1)(x-1)的值为( )
| A. | -6 | B. | 6 | C. | 18 | D. | 30 |



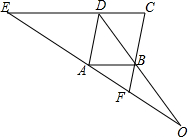 如图,已知EC∥AB,∠EDA=∠ABF.
如图,已知EC∥AB,∠EDA=∠ABF. 某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题:
某水果公司以2元/千克的成本购进10000千克柑橘,销售人员在销售过程中随机抽取柑橘进行“柑橘损坏率”统计,并绘制成如图所示的统计图,根据统计图提供的信息解决下面问题: