题目内容
11.已知A=$\frac{{{{({a+b})}^2}-4ab}}{{ab{{({a-b})}^2}}}$(ab≠0且a≠b)(1)化简A;
(2)若点P(a,b)在反比例函数y=-$\frac{5}{x}$的图象上,求A的值.
分析 (1)利用完全平方公式的展开式将(a+b)2展开,合并同类型、消元即可将A进行化解;
(2)由点P在反比例函数图象上,即可得出ab的值,代入A化解后的分式中即可得出结论.
解答 解:(1)A=$\frac{(a+b)^{2}-4ab}{ab(a-b)^{2}}$,
=$\frac{{a}^{2}+{b}^{2}+2ab-4ab}{ab(a-b)^{2}}$,
=$\frac{(a-b)^{2}}{ab(a-b)^{2}}$,
=$\frac{1}{ab}$.
(2)∵点P(a,b)在反比例函数y=-$\frac{5}{x}$的图象上,
∴ab=-5,
∴A=$\frac{1}{ab}$=-$\frac{1}{5}$.
点评 本题考查了分式的化解求值以及反比例函数图象上点的坐标特征,解题的关键是:(1)将原分式进行化解;(2)找出ab值.本题属于基础题,难度不大,解决该题型题目时,先将原分式进行化解,再代入ab求值即可.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
19.下列调查中,最适宜采用普查方式的是( )
| A. | 对我国初中学生视力状况的调查 | |
| B. | 对量子科学通信卫星上某种零部件的调查 | |
| C. | 对一批节能灯管使用寿命的调查 | |
| D. | 对“最强大脑”节目收视率的调查 |
6.下列计算正确的是( )
| A. | $\frac{x^2}{y^2}=\frac{x}{y}(y≠0)$ | B. | xy2÷$\frac{1}{2y}=2xy({y≠0})$ | ||
| C. | 2$\sqrt{x}+3\sqrt{y}=5\sqrt{xy}({x≥0,y≥0})$ | D. | (xy3)2=x2y6 |
9.圆心为P(m,n),半径为1的圆与平面直角坐标系的两坐标轴都相交,则m+n的值可能是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | 3 |
10.“十年树木,百年树人”,教师的素养关系到国家的未来.扬州市某区招聘音乐教师采用笔试、专业技能测试、说课三种形式进行选拔,这三项的成绩满分均为100分,并按2:3:5的比例折合纳入总分,最后,按照成绩的排序从高到低依次录取.该区要招聘2名音乐教师,通过笔试、专业技能测试筛选出前6名选手进入说课环节,这6名选手的各项成绩见表:
(1)笔试成绩的平均数是76;
(2)写出说课成绩的中位数为85.5,众数为85;
(3)已知序号为1,2,3,4号选手的总分成绩分别为84.2分,84.6分,88.1分,80.8分,请你判断这六位选手中序号是多少的选手将被录用?为什么?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 笔试成绩 | 66 | 90 | 86 | 64 | 66 | 84 |
| 专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
| 说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
(2)写出说课成绩的中位数为85.5,众数为85;
(3)已知序号为1,2,3,4号选手的总分成绩分别为84.2分,84.6分,88.1分,80.8分,请你判断这六位选手中序号是多少的选手将被录用?为什么?
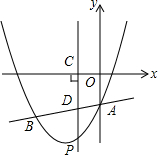 如图,抛物线y=x2+bx+c与直线y=$\frac{1}{2}$x-3交于A、B两点,其中点A在y轴上,点B坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
如图,抛物线y=x2+bx+c与直线y=$\frac{1}{2}$x-3交于A、B两点,其中点A在y轴上,点B坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.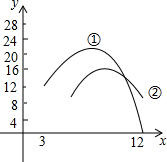 现有一生产季节性产品的企业,有两种营销方案,经测算:方案一一年中获得的每月利润y(万元)和月份x的关系为y=-0.5x2+8x-14,方案二一年中获得的每月利润y(万元)与月份x的关系为y=-x2+14x-24.两个函数部分图象如图所示:
现有一生产季节性产品的企业,有两种营销方案,经测算:方案一一年中获得的每月利润y(万元)和月份x的关系为y=-0.5x2+8x-14,方案二一年中获得的每月利润y(万元)与月份x的关系为y=-x2+14x-24.两个函数部分图象如图所示: