题目内容
13.不等式组$\left\{\begin{array}{l}{2x-1≥5}\\{8-4x<0}\end{array}\right.$的解集在数轴上表示为( )| A. |  | B. |  | C. | 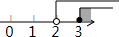 | D. |  |
分析 分别求出每一个不等式的解集,根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则即可得答案.
解答 解:$\left\{\begin{array}{l}{2x-1≥5}\\{8-4x<0}\end{array}\right.$,
解不等式2x-1≥5,得:x≥3,
解不等式8-4x<0,得:x>2,
故不等式组的解集为:x≥3,
故选:C.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟悉在数轴上表示不等式解集的原则“大于向右,小于向左,包括端点用实心,不包括端点用空心”是解题的关键.

练习册系列答案
相关题目
8.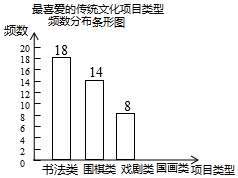 某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
 某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.最喜爱的传统文化项目类型频数分布表
| 项目类型 | 频数 | 频率 |
| 书法类 | 18 | a |
| 围棋类 | 14 | 0.28 |
| 喜剧类 | 8 | 0.16 |
| 国画类 | b | 0.20 |
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
 下列一串梅花图案是按一定规律排列的,请你仔细观察,在前2016个梅花图案中,共有504个“
下列一串梅花图案是按一定规律排列的,请你仔细观察,在前2016个梅花图案中,共有504个“ ”图案.
”图案.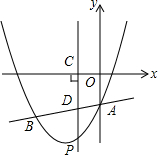 如图,抛物线y=x2+bx+c与直线y=$\frac{1}{2}$x-3交于A、B两点,其中点A在y轴上,点B坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
如图,抛物线y=x2+bx+c与直线y=$\frac{1}{2}$x-3交于A、B两点,其中点A在y轴上,点B坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D. 如图,扇形OAB的圆心角为120°,半径为3,则该扇形的弧长为2π.(结果保留π)
如图,扇形OAB的圆心角为120°,半径为3,则该扇形的弧长为2π.(结果保留π)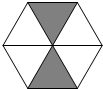 如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成,一只小鸟在广场上随机停留,刚好落在黑色三角形区域的概率为$\frac{1}{3}$.
如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成,一只小鸟在广场上随机停留,刚好落在黑色三角形区域的概率为$\frac{1}{3}$.