题目内容
1．若x=$\frac{y}{2}$=$\frac{z}{3}$，且x+2y-z=4，则x+y+z=12．分析 根据等式的性质，可用x表示y，用x表示z，根据解方程，可得x的值，根据代数式求值，可得答案．
解答 解：x=$\frac{y}{2}$=$\frac{z}{3}$，得
y=2x，z=3x．
x+2×2x-3x=4．
解得x=2，y=4，z=6．
x+y+z=2+4+6=12，
故答案为：12．
点评 本题考查了比例的性质，利用比例的性质得出y=2x，z=3x是解题关键．
练习册系列答案
相关题目
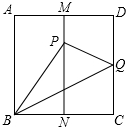如图，已知正方形纸片ABCD，M，N分别是AD、BC的中点，把BC边向上翻折，使点C恰好落在MN上的P点处，BQ为折痕，
12．不改变式子a-（2b-3c）的值，把式子中括号前“-”变成“+”结果应是（ ）
| A． | a+（2b-3c） | B． | a+（-2b-3c） | C． | a+（2b+3c） | D． | a+（-2b+3c） |