题目内容
11.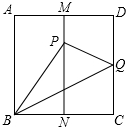 如图,已知正方形纸片ABCD,M,N分别是AD、BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,
如图,已知正方形纸片ABCD,M,N分别是AD、BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,(1)求∠PBQ的度数;
(2)若AB=1,求MP的长度.
分析 (1)根据折叠的性质可知:BN=$\frac{1}{2}$BP,从而可知∠BPN的值,再根据∠PBQ=∠CBQ,可将∠PBQ的角度求出∠PBQ的度数;
(2)由特殊锐角三角函数求得PN=$\frac{\sqrt{3}}{2}$,然后可求得PM的长.
解答 解:(1)根据折叠的性质知:BP=BC,∠PBQ=∠CBQ,
∴BN=$\frac{1}{2}$BC=$\frac{1}{2}$BP,
∵∠BNP=90°,
∴∠BPN=30°,
∴∠PBQ=$\frac{1}{2}$×60°=30°.
(2)在Rt△PBN中,PN=PB•sin60°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
MP=NM-PN=1-$\frac{\sqrt{3}}{2}$=$\frac{2-\sqrt{3}}{2}$.
点评 本题主要考查的是翻折的性质,掌握翻折的性质是解题的关键.

练习册系列答案
相关题目
 在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F.若△ADE的面积是1平方厘米.求△BEF的面积.
在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F.若△ADE的面积是1平方厘米.求△BEF的面积.