题目内容
12．某书店准备购进甲、乙两种图书共100本，购书款不高于2224元，预这100本图书全部售完的利润不低于1100元，两种图书的进价、售价如表所示：| 甲种图书 | 乙种图书 | |
| 进价（元/本） | 16 | 28 |
| 售价（元/本） | 26 | 40 |
（1）书店有多少种进书方案？
（2）在这批图书全部售出的条件下，（1）中的哪种方案利润最大？最大利润是多少？（请你用所学的函数知识来解决）
分析 （1）利用购书款不高于2224元，预计这100本图书全部售完的利润不低于1100元，结合表格中数据得出不等式组，求出即可；
（2）根据乙种书利润较高，故乙种书购进越多利润最大，故购进甲种书：48种，乙种书：52本利润最大求出即可；
解答 解：（1）设购进甲种图书x本，则购进乙书（100-x）本，根据题意得出：
$\left\{\begin{array}{l}{16x+28（100-x）≤2224}\\{10x+12（100-x）≥1100}\end{array}\right.$，
解得：48≤x≤50．
故有3种购书方案：甲种书：48本，乙种书：52本；甲种书：49本，乙种书：51本；甲种书：50本，乙种书：50本；
（2）根据乙种书利润较高，故乙种书购进越多利润最大，
故购进甲种书：48种，乙种书：52本利润最大为：48×（26-16）+52×（40-28）=1104（元）．
点评 此题主要考查了不等式组的应用以及二元一次方程的应用以及最佳方案问题，正确得出不等式关系是解题关键．
练习册系列答案
相关题目
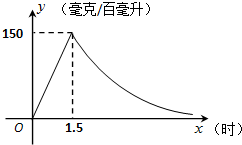实验数据显示，一般成人喝半斤低度白酒后，1.5小时内其血液中酒精含量y（毫克/百毫升）与时间x（时）成正比例；1.5小时后（包括1.5小时）y与x成反比例．根据图中提供的信息，解答下列问题：
一般情况下，学生注意力上课后逐渐增强，中间有段时间处于较理想的稳定状态，随后开始分散．实验结果表明，学生注意力指数y随时间x（min）的变化规律如图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：
17．
已知：如图在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线y=$\frac{k}{x}$（x＞0）经过D点，交BC的延长线于E点，且OB•AC=160，则点E的坐标为（ ）
已知：如图在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线y=$\frac{k}{x}$（x＞0）经过D点，交BC的延长线于E点，且OB•AC=160，则点E的坐标为（ ）| A． | （5，8） | B． | （5，10） | C． | （4，8） | D． | （3，10） |
如图，已知点B，D在反比例函数y=$\frac{a}{x}$（a＞0）的图象上，点A，C在反比例函数y=$\frac{b}{x}$（b＜0）的图象上，AB∥CD∥x轴，AB，CD在x轴的同侧，AB=4，CD=3，AB与CD的距离为1，则a-b的值是12．