题目内容
11.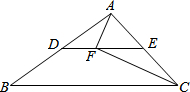 如图,在△ABC中,BC=10,点D,E分别是AB,AC的中点.点F是线段DE上一
如图,在△ABC中,BC=10,点D,E分别是AB,AC的中点.点F是线段DE上一动点.当DF=2时,∠AFC恰好为90°,则AC长为6.
分析 根据三角形中位线定理得到DE=5,易求EF的长度;然后根据直角△AFC斜边上的中线等于斜边的一半来求AC的长度.
解答 解:∵点D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,且DE=$\frac{1}{2}$BC=5.
又∵BC=10,
∴DE=5.
∵DF=2,
∴EF=3.
又∵∠AFC恰好为90°,F是AG的中点,
∴EF是斜边AC上的中线,
∴AC=2EF=6.
故答案是:6.
点评 本题主要考查对三角形的中位线定理、直角三角形斜边上的中线的理解和掌握,能正确运用三角形的中位线定理进行计算是解此题的关键.

练习册系列答案
相关题目
6.某市70%的家庭年收入不少于3万元,下面一定不少于3万元的是( )
| A. | 年收入的平均数 | B. | 年收入的中位数 | ||
| C. | 年收入的众数 | D. | 年收入的平均数和众数 |
1.2014年德州市农村中小学校含标准化工程开工学校项目356个,开工面积56.2万平方米,开式面积量创历年最高,56.2万平方米用科学记数法表示正确的是( )
| A. | 5.62×104m2 | B. | 56.2×104m2 | C. | 5.62×105m2 | D. | 0.562×104m2 |
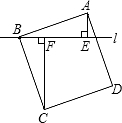 如图,过正方形ABCD的顶点B作直线l,过点A、C作l的垂线,垂足分别为点E、F,若AE=1,CF=2,求正方形的面积.
如图,过正方形ABCD的顶点B作直线l,过点A、C作l的垂线,垂足分别为点E、F,若AE=1,CF=2,求正方形的面积.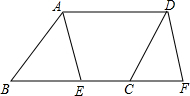 在?ABCD中,点E在边BC上,点F在BC的延长线上,且EF=AD.
在?ABCD中,点E在边BC上,点F在BC的延长线上,且EF=AD. 在平面直角坐标系中,点A是抛物线y=a(x-4)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为24.
在平面直角坐标系中,点A是抛物线y=a(x-4)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为24.