题目内容
2.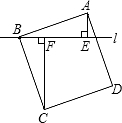 如图,过正方形ABCD的顶点B作直线l,过点A、C作l的垂线,垂足分别为点E、F,若AE=1,CF=2,求正方形的面积.
如图,过正方形ABCD的顶点B作直线l,过点A、C作l的垂线,垂足分别为点E、F,若AE=1,CF=2,求正方形的面积.
分析 由正方形的性质得出AB=BC=CD=DA,∠ABC=90°,得出∠CBF+∠ABE=90°,证出∠BAE=∠CBF,由AAS证明△BFC≌△AEB,得出BF=AE=1,再根据勾股定理求出BC2,即可得出正方形的面积.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=90°,
∴∠CBF+∠ABE=90°,
∵AE⊥l,CF⊥l,
∴∠AEB=∠CFB=90°,
∴∠ABE+∠BAE=90°,
∴∠BAE=∠CBF,
在△BFC和△AEB中,$\left\{\begin{array}{l}{∠CFB=∠AEB}&{\;}\\{∠CBF=∠BAE}&{\;}\\{BC=AB}&{\;}\end{array}\right.$,
∴△BFC≌△AEB(AAS),
∴BF=AE=1,
∴BC2=BF2+CF2=12+22=5,
∴S正方形ABCD=BC2=5.
点评 本题考查了正方形的性质、全等三角形的判定与性质、勾股定理以及正方形面积的计算;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
7.若点P(x,y)在第一象限,则点Q(x+y,x-y)一定不在( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第二、三象限 | D. | 第二、四象限 |
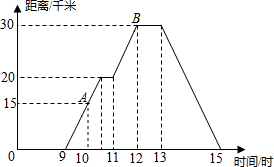 小明家在下白石,他很想一个人去穆阳白云山玩,不过他要先到赛岐停留下,然后在接着去穆阳白云山,他把一天的时间做了一个规划,下面是小明一天从0点到15点的离家距离的情况.
小明家在下白石,他很想一个人去穆阳白云山玩,不过他要先到赛岐停留下,然后在接着去穆阳白云山,他把一天的时间做了一个规划,下面是小明一天从0点到15点的离家距离的情况.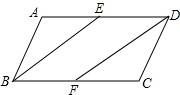 如图,在?ABCD中,点E、F分别在边AD,BC上,且BE∥DF.若∠EBF=50°,则∠EDF的度数是50°.
如图,在?ABCD中,点E、F分别在边AD,BC上,且BE∥DF.若∠EBF=50°,则∠EDF的度数是50°.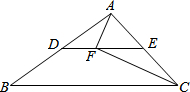 如图,在△ABC中,BC=10,点D,E分别是AB,AC的中点.点F是线段DE上一
如图,在△ABC中,BC=10,点D,E分别是AB,AC的中点.点F是线段DE上一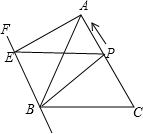 如图,在△ABC中,AB=AC=13cm,BC=10cm,BF∥AC,动点P从点C出发以2cm/s的速度沿CA向终点A移动,过P作PE∥BC交BF于点E,设动点P的运动时间为t秒.
如图,在△ABC中,AB=AC=13cm,BC=10cm,BF∥AC,动点P从点C出发以2cm/s的速度沿CA向终点A移动,过P作PE∥BC交BF于点E,设动点P的运动时间为t秒.