题目内容
 如图,四边形ABCD是平行四边形,顶点A、B的坐标分别是A(1,0),B(0,-2),顶点C、D在双曲线y=
如图,四边形ABCD是平行四边形,顶点A、B的坐标分别是A(1,0),B(0,-2),顶点C、D在双曲线y=| k |
| x |
| A、-16 | B、-9 |
| C、-8 | D、-12 |
考点:平行四边形的性质,反比例函数图象上点的坐标特征
专题:
分析:分别过C、D作x轴的垂线,垂足为F、G,过C点作CH⊥DG,垂足为H,根据CD∥AB,CD=AB可证△CDH≌△ABO,则CH=AO=1,DH=OB=2,由此设C(m+1,n),D(m,n+2),C、D两点在双曲线上,则(m+1)n=m(n+2),解得n=2m,设直线AD解析式为y=ax+b,将A、D两点坐标代入求解析式,确定E点坐标,求S△ABE,根据S四边形BCDE=5S△ABE,列方程求m、n的值,根据k=(m+1)n求解.
解答:解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
在△CDH和△ABO中,
,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2,
设C(m+1,n),D(m,n+2),
则(m+1)n=m(n+2)=k,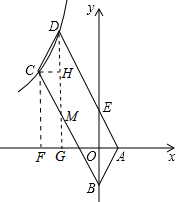
解得n=2m,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得
,
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则
,
∴y=-2x+2,
∴E(0,2),BE=4,
∴S△ABE=
×BE×AO=2,
∵S四边形BCDE=5S△ABE=5×
×4×1=10,
∵S四边形BCDE=S△ABE+S四边形BEDM=10,
即2+4×m=10,
解得:m=2,
∴n=2m=4,
∴|k|=(m+1)n=12.
∵双曲线图形在第二象限,
∴k=-12
故选D.
∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
在△CDH和△ABO中,
|
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2,
设C(m+1,n),D(m,n+2),
则(m+1)n=m(n+2)=k,

解得n=2m,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得
|
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则
|
∴y=-2x+2,
∴E(0,2),BE=4,
∴S△ABE=
| 1 |
| 2 |
∵S四边形BCDE=5S△ABE=5×
| 1 |
| 2 |
∵S四边形BCDE=S△ABE+S四边形BEDM=10,
即2+4×m=10,
解得:m=2,
∴n=2m=4,
∴|k|=(m+1)n=12.
∵双曲线图形在第二象限,
∴k=-12
故选D.
点评:本题考查了反比例函数的综合运用.关键是通过作辅助线,将图形分割,寻找全等三角形,利用边的关系设双曲线上点的坐标,根据面积关系,列方程求解.

练习册系列答案
相关题目
一次函数y=kx+b的图象经过点(m2+1,1)和(-1,m2+1)(m≠0),则k、b应满足的条件是( )
| A、k>0,b>0 |
| B、k>0,b<0 |
| C、k<0,b<0 |
| D、k<0,b>0 |
下列运算正确的是( )
| A、a2+a=a3 |
| B、a2•a=a3 |
| C、a2÷a=2 |
| D、(2a)2=4a |
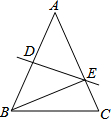 如图,将△ABC沿直线DE折叠,使得点A与点B重合,已知AC=8cm,△BCE的周长为13cm,则BC的长为( )
如图,将△ABC沿直线DE折叠,使得点A与点B重合,已知AC=8cm,△BCE的周长为13cm,则BC的长为( )| A、5cm | B、6cm |
| C、8cm | D、10cm |
 如图,已知∠1+∠2=180°,还需要添加条件∠3=
如图,已知∠1+∠2=180°,还需要添加条件∠3=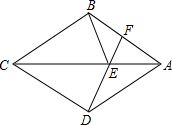 已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.