题目内容
4.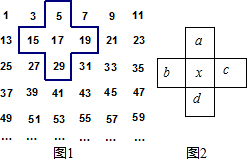 如图,将连续的奇数1,3,5,7,…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
如图,将连续的奇数1,3,5,7,…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.(1)若x=17,则a+b+c+d=68.
(2)用含x的式子分别表示数a,b,c,d.
(3)直接写出a,b,c,d,x这5个数之间的一个等量关系:a+b+c+d=4x.
(4)设M=a+b+c+d+x,判断M的值能否等于2010,请说明理由.
分析 (1)由x=17可找出a、b、c、d的值,将其相加即可得出结论;
(2)根据图形即可得出a、b、c、d与x之间的关系;
(3)由(2)的结论,将a、b、c、d相加即可得出结论;
(4)根据M=5x,代入2010求出x的值,根据x的奇偶性即可得出M的值不能等于2010.
解答 解:(1)∵x=17,
∴a=x-12=5,d=x+12=29,b=x-2=15,c=x+2=19,
∴a+b+c+d=5+15+19+29=68.
故答案为:68.
(2)根据数的排列结合十字框的框法,即可得出:
a=x-12,b=x-2,c=x+2,d=x+12.
(3)∵a+d=x-12+x+12=2x,b+c=x-2+x+2=2x,
∴a+b+c+d=4x.
故答案为:a+b+c+d=4x.
(4)不能等于2010,理由如下:
∵a+b+c+d=4x,
∴M=a+b+c+d+x=5x.
当5x=2010时,x=402,
∵402为偶数,而数表中的所有数为奇数,
∴M的值不能等于2010.
点评 本题考查了一元一次方程的应用以及列代数式,解题的关键:(1)根据x=17找出a、b、c、d的值;(2)根据十字框框住五个数的特点,用含x的式子分别表示数a,b,c,d;(3)将a、b、c、d相加;(4)令M=5x=2010,求出x值.

练习册系列答案
相关题目
12.某县以“重点整治环境卫生”为抓手,加强对各乡镇环保建设的投入,计划从2017年起到2019年累计投入4250万元,已知2017年投入1500万元,设投入经费的年平均增长率为x,根据题意,下列所列方程正确的是( )
| A. | 1500(1+x)2=4250 | B. | 1500(1+2x)=4250 | ||
| C. | 1500+1500x+1500x2=4250 | D. | 1500(1+x)+1500(1+x)2=4250-1500 |
19.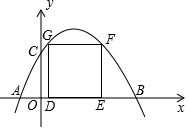 如图,抛物线l与坐标轴的交点为A(-1,0),B(4,0),C(0,2),四边形DEFG是正方形,且点D,E在x轴上,点F,G在抛物线上,则正方形DEFG的面积为57±8$\sqrt{41}$.
如图,抛物线l与坐标轴的交点为A(-1,0),B(4,0),C(0,2),四边形DEFG是正方形,且点D,E在x轴上,点F,G在抛物线上,则正方形DEFG的面积为57±8$\sqrt{41}$.
 如图,抛物线l与坐标轴的交点为A(-1,0),B(4,0),C(0,2),四边形DEFG是正方形,且点D,E在x轴上,点F,G在抛物线上,则正方形DEFG的面积为57±8$\sqrt{41}$.
如图,抛物线l与坐标轴的交点为A(-1,0),B(4,0),C(0,2),四边形DEFG是正方形,且点D,E在x轴上,点F,G在抛物线上,则正方形DEFG的面积为57±8$\sqrt{41}$.
16.以下列各组数据为三角形的三边,能构成直角三角形的是( )
| A. | 4cm,8cm,7cm | B. | 2cm,2cm,2cm | C. | 2cm,2cm,4cm | D. | 6cm,8cm,10cm |
 如图,海中有一个小岛B,它的周围14海里内有暗礁,在小岛正西方有一点A测得在北偏东60°,方向上有一灯塔C,灯塔C在小岛B北偏东15°方向上20海里处,渔船跟踪鱼群沿AC方向航行,每小时航行10$\sqrt{2}$海里.
如图,海中有一个小岛B,它的周围14海里内有暗礁,在小岛正西方有一点A测得在北偏东60°,方向上有一灯塔C,灯塔C在小岛B北偏东15°方向上20海里处,渔船跟踪鱼群沿AC方向航行,每小时航行10$\sqrt{2}$海里. 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若$\frac{AD}{AB}$=$\frac{4}{5}$,DE=8,则BC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若$\frac{AD}{AB}$=$\frac{4}{5}$,DE=8,则BC等于( ) 如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.