题目内容
5.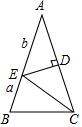 如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b的代数式表示△ABC的周长为2a+3b.
如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b的代数式表示△ABC的周长为2a+3b.
分析 由题意可知:AC=AB=a+b,由于DE是线段AC的垂直平分线,∠BAC=36°,所以易证AE=CE=BC=b,从可知△ABC的周长;
解答 解:∵AB=AC,
BE=a,AE=b,
∴AC=AB=a+b,
∵DE是线段AC的垂直平分线,
∴AE=CE=b,
∴∠ECA=∠BAC=36°,
∵∠BAC=36°,
∴∠ABC=∠ACB=72°,
∴∠BCE=∠ACB-∠ECA=36°,
∴∠BEC=180°-∠ABC-∠ECB=72°,
∴CE=BC=b,
∴△ABC的周长为:AB+AC+BC=2a+3b
故答案为:2a+3b.
点评 本题考查线段垂直平分线的性质,解题的关键是利用等腰三角形的性质以及垂直平分线的性质得出AE=CE=BC,本题属于中等题型.

练习册系列答案
相关题目
15.下列4个图形中,是中心对称图形但不是轴对称的图形是( )
| A. |  | B. |  | C. |  | D. |  |
20. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )
如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )
 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )
如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )| A. | $\frac{h}{sinα}$ | B. | $\frac{h}{cosα}$ | C. | $\frac{h}{tanα}$ | D. | h•cosα |
10.下列实数中,为有理数的是( )
| A. | $\sqrt{3}$ | B. | π | C. | $\root{3}{2}$ | D. | 1 |
17. 如图,已知直线a∥b,直线c分别与a,b相交,∠1=110°,则∠2的度数为( )
如图,已知直线a∥b,直线c分别与a,b相交,∠1=110°,则∠2的度数为( )
 如图,已知直线a∥b,直线c分别与a,b相交,∠1=110°,则∠2的度数为( )
如图,已知直线a∥b,直线c分别与a,b相交,∠1=110°,则∠2的度数为( )| A. | 60° | B. | 70° | C. | 80° | D. | 110° |
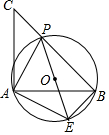 如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.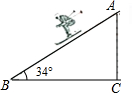 如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了280米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了280米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)