题目内容
16.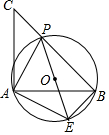 如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求PC2+PB2的值.
分析 (1)只要证明∠AEP=∠ABP=45°,∠PAB=90°即可解决问题;
(2)作PM⊥AC于M,PN⊥AB于N,则四边形PMAN是矩形,可得PM=AN,由△PCM,△PNB都是等腰直角三角形,推出PC=$\sqrt{2}$PM,PB=$\sqrt{2}$PN,可得PC2+PB2=2(PM2+PN2)=2(AN2+PN2)=2PA2=PE2=22=4;
解答 (1)证明: ∵AB=AC,∠BAC=90°,
∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
∴∠AEP=∠ABP=45°,
∵PE是直径,
∴∠PAB=90°,
∴∠APE=∠AEP=45°,
∴AP=AE,
∴△PAE是等腰直角三角形.
(2)作PM⊥AC于M,PN⊥AB于N,则四边形PMAN是矩形,
∴PM=AN,
∵△PCM,△PNB都是等腰直角三角形,
∴PC=$\sqrt{2}$PM,PB=$\sqrt{2}$PN,
∴PC2+PB2=2(PM2+PN2)=2(AN2+PN2)=2PA2=PE2=22=4.
(也可以证明△ACP≌△ABE,△PBE是直角三角形)
点评 本题考查三角形的外接圆与外心、勾股定理、矩形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考常考题型.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
6.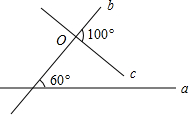 平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )
平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )
 平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )
平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a垂直,则旋转的最小度数是( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
7.一张矩形纸片ABCD,已知AB=3,AD=2,小明按如图步骤折叠纸片,则线段DG长为( )
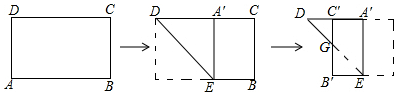

| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 1 | D. | 2 |
4. 小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
 小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )
小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是( )| A. | (-2,1) | B. | (-1,1) | C. | (1,-2) | D. | (-1,-2) |
1. 如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
 如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )| A. | -6 | B. | 6 | C. | 0 | D. | 无法确定 |
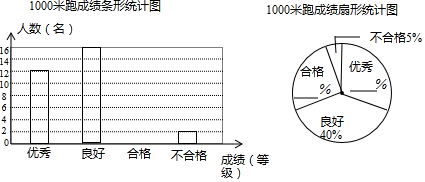
6. 某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
请解答下列问题:
(1)a=36,b=9;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为90°;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.
 某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.| 社团名称 | 人数 |
| 文学社团 | 18 |
| 科技社团 | a |
| 书画社团 | 45 |
| 体育社团 | 72 |
| 其他 | b |
(1)a=36,b=9;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为90°;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.
 如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.
如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.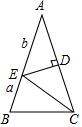 如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b的代数式表示△ABC的周长为2a+3b.
如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b的代数式表示△ABC的周长为2a+3b.