题目内容
20. 如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )
如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A、D、B在同一条直线上)( )| A. | $\frac{h}{sinα}$ | B. | $\frac{h}{cosα}$ | C. | $\frac{h}{tanα}$ | D. | h•cosα |
分析 根据同角的余角相等得∠CAD=∠BCD,由os∠BCD=$\frac{CD}{BC}$知BC=$\frac{CD}{cos∠BCD}$=$\frac{h}{cosα}$.
解答 解:∵∠CAD+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠CAD=∠BCD,
在Rt△BCD中,∵cos∠BCD=$\frac{CD}{BC}$,
∴BC=$\frac{CD}{cos∠BCD}$=$\frac{h}{cosα}$,
故选:B.
点评 本题主要考查解直角三角形的应用,熟练掌握同角的余角相等和三角函数的定义是解题的关键.

练习册系列答案
相关题目
10.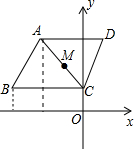 如图,平行四边形ABCD的顶点A(-2,3),B(-3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( )
如图,平行四边形ABCD的顶点A(-2,3),B(-3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( )
 如图,平行四边形ABCD的顶点A(-2,3),B(-3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( )
如图,平行四边形ABCD的顶点A(-2,3),B(-3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( )| A. | (-2017,2) | B. | (-2017,-2) | C. | (-2018,-2) | D. | (-2018,2) |
12.在下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  直角三角形 | B. |  正五边形 | C. |  正方形 | D. |  平行四边形 |
9.点P(1,-2)关于y轴对称的点的坐标是( )
| A. | (1,2) | B. | (-1,2) | C. | (-1,-2) | D. | (-2,1) |
 如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.
如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.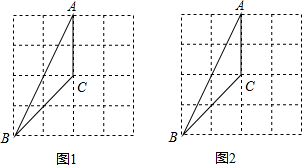
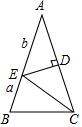 如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b的代数式表示△ABC的周长为2a+3b.
如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a、b的代数式表示△ABC的周长为2a+3b.