题目内容
2.下列各式计算正确的是( )| A. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | B. | 5$\sqrt{6}$-3$\sqrt{3}$=2$\sqrt{3}$ | C. | ($\sqrt{8}$+$\sqrt{50}$)÷2=$\sqrt{4}$+$\sqrt{25}$=7 | D. | 3$\sqrt{3}$+$\sqrt{27}$=6$\sqrt{3}$ |
分析 直接利用二次根式的加减运算法则化简求出答案.
解答 解:A、$\sqrt{5}$+$\sqrt{2}$无法计算,故此选项错误;
B、5$\sqrt{6}$-3$\sqrt{3}$无法计算,故此选项错误;
C、($\sqrt{8}$+$\sqrt{50}$)÷2=$\frac{7\sqrt{2}}{2}$,故此选项错误;
D、3$\sqrt{3}$+$\sqrt{27}$=6$\sqrt{3}$,正确.
故选:D.
点评 此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
13.阿伟的游戏机充满电后,可用来连续播放音乐36个小时或连续玩游戏6个小时,若游戏机在早上7点充满电后,阿伟马上使用游戏机播放音乐直到下午3点,并从下午3点继续使用游戏机玩游戏直到它没电,则他的游戏机何进没电?( )
| A. | 晚上7点20分 | B. | 晚上8点20分 | C. | 晚上7点40分 | D. | 晚上8点40分 |
10.|2|的相反数为( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
17.下列运算正确的是( )
| A. | (-3)2=-9 | B. | (-1)2017×(-1)=1 | C. | -9÷3=3 | D. | -|-1|=1 |
14.下面是一位同学做的四道题:
①2a+3b=5ab;
②-(-2a2b3)4=-16a8b12;
③(a+b)3=a3+b3;
④(a-2b)2=a2-2ab+4b2
其中做对的一道题的序号是( )
①2a+3b=5ab;
②-(-2a2b3)4=-16a8b12;
③(a+b)3=a3+b3;
④(a-2b)2=a2-2ab+4b2
其中做对的一道题的序号是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
11.下列各式中,计算过程正确的是( )
| A. | $\sqrt{{2^2}+{7^2}}$=2+7 | B. | $\sqrt{9\frac{1}{2}}$=3$\sqrt{\frac{1}{2}}$ | C. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | D. | $\frac{{\sqrt{8}+\sqrt{12}}}{{\sqrt{2}}}$=4+6 |
12.将直线y=2x-4向上平移5个单位长度后,所得直线的表达式是( )
| A. | y=2x-9 | B. | y=2x-5 | C. | y=2x+5 | D. | y=2x+1 |
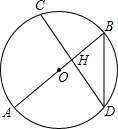 如图,AB是⊙O的直径,弦CD⊥AB于H,且CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则AB的长为( )
如图,AB是⊙O的直径,弦CD⊥AB于H,且CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则AB的长为( )