题目内容
9．已知关于x的方程x2+2x-（m-2）=0有两个不相等的实数根，则m的取值范围是（ ）| A． | m≥1 | B． | m≤1 | C． | m＞1 | D． | m＜1 |
分析 关于x的方程x2+2x-（m-2）=0有两个不相等的实数根，即判别式△=b2-4ac＞0，即可得到关于m的不等式，从而求得m的范围．
解答 解：∵关于x的方程x2+2x-（m-2）=0有两个不相等的实数根，
∴△=b2-4ac=22+4×1×（m-2）=4m-4＞0，
解得：m＞1．
故选C．
点评 本题考查了根的判别式，一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：
①当△＞0时，方程有两个不相等的两个实数根；②当△=0时，方程有两个相等的两个实数根；
③当△＜0时，方程无实数根．上面的结论反过来也成立．
练习册系列答案
新课标同步训练系列答案
相关题目
19．如图1，在平面直角坐标系中，将?ABCD放置在第一象限，且AB∥x 轴．直线y=-x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示，则□ABCD的面积为（ ）
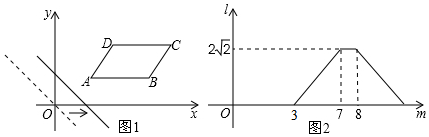
| A． | 10 | B． | 10$\sqrt{5}$ | C． | 5 | D． | 5$\sqrt{5}$ |
20．篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分．某队预计在2016-2017赛季全部32场比赛中最少得到48分，才有希望进入季后赛．假设这个队在将要举行的比赛中胜x场，要达到目标，x应满足的关系式是（ ）
| A． | 2x+（32-x）≥48 | B． | 2x-（32-x）≥48 | C． | 2x+（32-x）≤48 | D． | 2x≥48 |
17．
小邢到单位附近的加油站加油，如图是小邢所用的加油机上的数据显示牌，则数据中的变量是（ ）
小邢到单位附近的加油站加油，如图是小邢所用的加油机上的数据显示牌，则数据中的变量是（ ）| A． | 金额 | B． | 数量 | C． | 单价 | D． | 金额和数量 |
4．计算：（-5）+3的结果是（ ）
| A． | -8 | B． | -2 | C． | 2 | D． | 8 |
14．一个角的余角是它的2倍，这个角的度数是（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
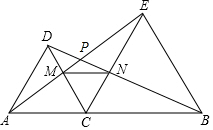如图，点C为线段AB上一点，△DAC、△ECB都是等边三角形，AE、DC交于点M，DB、EC交于点N，DB、AE交于点P，连接MN，下列说法正确的个数有（ ）
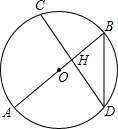如图，AB是⊙O的直径，弦CD⊥AB于H，且CD=2$\sqrt{2}$，BD=$\sqrt{3}$，则AB的长为（ ）