题目内容
2.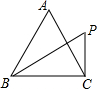 如图,在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
如图,在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
分析 根据等边三角形的角平分线的性质可以得出AP就是所求的距离,以及AP=CP,然后在直角三角形PBC中求得PC的长,即可求得答案.
解答 解:∵在边长为3的等边△ABC中,过点C作垂直于BC的直线交∠ABC的平分线于点P,
∴BP交AC于点D,且BD⊥AD,AD=DC,
∴BC=3,∠PBC=30°,∠PBC=90°,∠ACP=30°,
∴BP=2$\sqrt{3}$,PC=$\sqrt{3}$,
连接AP,则△BAP≌△BCP,
∴∠PAC=∠PCB=90°,
∴点P到边AB所在直线的距离为AP的长,
又∵PC=$\sqrt{3}$,
∴PA=PC=$\sqrt{3}$,
故选:D.
点评 本题主要考查了等边三角形的性质:等边三角形的三个内角都相等,且都等于60°;等边三角形是轴对称图形,它有三条对称轴;它的任意一角的平分线都垂直平分对边,三边的垂直平分线是对称轴;角平分线的性质:角的平分线上的点到角的两边的距离相等.注意:①这里的距离是指点到角的两边垂线段的长;②该性质可以独立作为证明两条线段相等的依据,有时不必证明全等;③使用该结论的前提条件是图中有角平分线.

练习册系列答案
相关题目
13.已知ab>0,bc<0,则直线y=-$\frac{a}{b}$x+$\frac{a}{c}$经过的象限为( )
| A. | 一、二、三 | B. | 一、二、四 | C. | 二、三、四 | D. | 一、二、四 |
7.y=-(x+1)2+k上有A(-$\sqrt{2}$,y1),B($\sqrt{2}$,y2)两点,则y1,y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1≤y2 |
11.在△ACB中,AB=10,sinA=$\frac{3}{5}$,则BC的长为( )
| A. | 6 | B. | 7.5 | C. | 8 | D. | 不能确定 |
12.下列方程中,是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | x2-y-1=0 | C. | $\frac{1}{x}$+x=1 | D. | x2=2 |
