题目内容
19.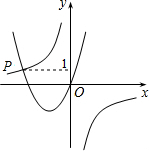 如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解为( )
如图,已知函数y=-$\frac{3}{x}$与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+$\frac{3}{x}$=0的解为( )| A. | x=3 | B. | x=1 | C. | x=-3 | D. | 无解 |
分析 先求出P点坐标,再把方程的解转化为求两函数的交点问题,进而可得出结论.
解答 解:∵函数y=-$\frac{3}{x}$经过点P,点P的纵坐标为1,
∴1=-$\frac{3}{x}$,解得x=-3.
∵ax2+bx+$\frac{3}{x}$=0可化为方程ax2+bx=-$\frac{3}{x}$,
∴此方程的解即为两函数的交点,
∴x=-3.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,解答此题的关键是把求方程的解转化为求函数交点的问题是解答此题的关键.

练习册系列答案
相关题目
7.y=-(x+1)2+k上有A(-$\sqrt{2}$,y1),B($\sqrt{2}$,y2)两点,则y1,y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1≤y2 |
4.某广场地面铺满了边长为36cm的正六边形地砖,现在向上抛掷半径为6$\sqrt{3}$cm的圆碟,圆碟落地后与地砖间的间隙不相交的概率为( )
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
11.在△ACB中,AB=10,sinA=$\frac{3}{5}$,则BC的长为( )
| A. | 6 | B. | 7.5 | C. | 8 | D. | 不能确定 |
9.从多边形的一个顶点出发,连接其它各个顶点得到2016个三角形,则这个多边形的边数为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |

 在如图所示的运算程序中,如果输出的数y=6,则输入的数x=2或9.
在如图所示的运算程序中,如果输出的数y=6,则输入的数x=2或9.