题目内容
15.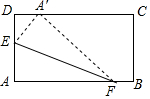 如图,折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,已知AD=3,AF=5,则AE的长是( )
如图,折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,已知AD=3,AF=5,则AE的长是( )| A. | $\frac{5}{3}$ | B. | $\frac{8}{5}$ | C. | $\sqrt{3}$ | D. | $\frac{2}{3}$$\sqrt{5}$ |
分析 过F作FG⊥CD于G,则FG=BC=AD=3,根据折叠的性质得到AE=A′E,A′F=AF=5,根据勾股定理得到A′G=$\sqrt{A′{F}^{2}-F{G}^{2}}$=4,然后根据勾股定理列方程即可得到结论.
解答  解:过F作FG⊥CD于G,
解:过F作FG⊥CD于G,
则FG=BC=AD=3,
∵折叠矩形ABCD的一角A,使得点A落在CD边上的点A′处,
∴AE=A′E,A′F=AF=5,
∴A′G=$\sqrt{A′{F}^{2}-F{G}^{2}}$=4,
∴A′D=1,
∵DE=AD-AE=3-AE,
∵DE2=A′E2-A′D2,
∴(3-AE)2=AE2-12,
∴AE=$\frac{5}{3}$,
故选A.
点评 此题考查了翻折变换的知识,根据已知条件表示出每条线段的长度,然后利用勾股定理进行解答,有一定难度.

练习册系列答案
相关题目
6.下列命题中,真命题是( )
| A. | 垂直于同一条直线的两条直线互相平行 | |
| B. | 两条平行直线被第三条直线所截,则一组同旁内角的平分线互相垂直 | |
| C. | 三角形的一个外角等于两个内角的和 | |
| D. | 等边三角形既是中心对称图形,又是轴对称图形 |
3.(-8)2016+(-8)2015能被下列数整除的是( )
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
10.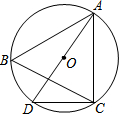 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,则∠B的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,则∠B的度数是( )
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,则∠B的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,则∠B的度数是( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
20.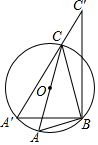 在半径为7的圆O中,AC为其直径,点B是圆上的定点,∠ACB=30°,点A′在$\widehat{AC}$上运动(不与A,C重合),C′B⊥A′B交A′C的延长线于点C′,则BC′最大值为 ( )
在半径为7的圆O中,AC为其直径,点B是圆上的定点,∠ACB=30°,点A′在$\widehat{AC}$上运动(不与A,C重合),C′B⊥A′B交A′C的延长线于点C′,则BC′最大值为 ( )
 在半径为7的圆O中,AC为其直径,点B是圆上的定点,∠ACB=30°,点A′在$\widehat{AC}$上运动(不与A,C重合),C′B⊥A′B交A′C的延长线于点C′,则BC′最大值为 ( )
在半径为7的圆O中,AC为其直径,点B是圆上的定点,∠ACB=30°,点A′在$\widehat{AC}$上运动(不与A,C重合),C′B⊥A′B交A′C的延长线于点C′,则BC′最大值为 ( )| A. | 14 | B. | 21 | C. | 14$\sqrt{3}$ | D. | 21$\sqrt{3}$ |
7.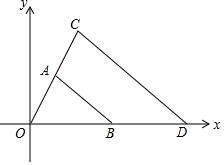 如图,△AOB和△COD是以点O为位似中心的位似图形,点A的坐标为(1,2),点B的坐标为(3,0),相似比为1:2,则点C的坐标为( )
如图,△AOB和△COD是以点O为位似中心的位似图形,点A的坐标为(1,2),点B的坐标为(3,0),相似比为1:2,则点C的坐标为( )
 如图,△AOB和△COD是以点O为位似中心的位似图形,点A的坐标为(1,2),点B的坐标为(3,0),相似比为1:2,则点C的坐标为( )
如图,△AOB和△COD是以点O为位似中心的位似图形,点A的坐标为(1,2),点B的坐标为(3,0),相似比为1:2,则点C的坐标为( )| A. | (2,3) | B. | (2,4) | C. | (3,3) | D. | (3,4) |
20.下面能判断两个三角形全等的条件是( )
| A. | 有两边及其中一边所对的角对应相等 | |
| B. | 三个角对应相等 | |
| C. | 两边和它们的夹角对应相等 | |
| D. | 两个三角形周长相等 |